Using Homogenized Models to Explore the Effect of Fracture Densities on Weathering

1. INTRODUCTION

An important next step toward understanding the development of porosity in the Earth’s near surface and how it acts to store or transport water is to understand how rock heterogeneities affect weathering (Brantley et al., 2017; Gu et al., 2020). One of the most common examples of heterogeneity is the presence of fractures, and the development of models to simulate fractured systems has been a goal that was recognized as early as 2001 (Xu et al., 2001; Xu & Pruess, 2001). This goal is taking on increasing importance now with the availability of new geophysical data exploring the critical zone (Clarke & Burbank, 2011; St. Clair et al., 2015). In particular, St. Clair and others emphasize that “the base of the weathered zone is the depth above which stresses allow abundant fractures to grow or open…” Clarke and Burbank explicitly address two geological systems in New Zealand, one where fracture density is constant with depth and one where it is not constant with depth. The former was attributed to tectonic drivers of fracturing (Southern Alps of New Zealand) and the latter was attributed to the overprinting of geomorphological drivers of fracturing on top of tectonically driven fractures (Fiordland, New Zealand). Given the apparent co-location of fractures and weathering identified in that and other studies, many questions are coming into focus concerning how and why such opening of fractures are coupled to weathering. To make such questions even more complex, we note that water flow in hills must also cause and be affected by both weathering and fractures (for example, Brantley et al., 2017; Ma et al., 2021; Rempe & Dietrich, 2018). As a first step to understand fracturing, water flow, and weathering in hills, we therefore identified three important questions to explore with simulations in this paper: How is weathering affected by changes in fracture density beneath a hillslope? How is the rate of weathering of a fractured hillside affected by lateral subsurface flow? How does weathering affect the depth of the water table in a fractured hill compared to an unfractured hill?

To address such questions about fractures, fluid flow, and weathering may require numerical simulations to couple these phenomena. However, such simulations are technically difficult (see Background) and many techniques have been explored with varying success. Here, we use the method of homogenization (Hornung, 1997). This technique entails starting from a micro-or meso-model and proceeding to some version of a macro-model. We apply this method to investigate aspects of weathering of fractured systems in the context of the three questions. For each question we also explore whether the homogenized model can be used for the system of interest. Our approach explicitly couples reaction and its effect on fluid flow and explores unsaturated versus saturated flow as well as eroding and non-eroding hillsides.

2. BACKGROUND

Methods to simulate weathering in natural media span from parsimonious models of simplified systems (for example, Lebedeva et al., 2010; Lichtner, 1988) to reactive transport models that are fully-parameterized for all major components and phases (for example, Xu & Pruess, 2001). These different approaches have different attributes and drawbacks. The homogenization approach utilized here lies more in the realm of simplified parsimonious models. Such parsimonious models provide the benefit that they do not require quantification of as many parameters as a full reactive transport model. Using homogenization approaches nonetheless can elucidate how a system operates and may lead to better conceptual models for upscaling (Wen et al., 2021).

In contrast to the homogenization approach, another common approach used to model fractured system is a dual-porosity approximation (Barenblatt et al., 1960; Gerke & Van Genuchten, 1993a, 1993b; Xu et al., 2001; Xu & Pruess, 2001). This approach assumes that the medium consists of two regions: i) the network of fractures and ii) the individual rock-matrix blocks. Unlike the method of homogenization which considers the heterogeneous medium as a new homogeneous medium with effective properties, the dual-porosity method considers two continua (fractures and rock-matrices) that comprise every point of the structured system. These continua interact with each other. The main difficulty in such a treatment is to derive terms describing this interaction. In addition, such a method poses difficulties in visualization or in application to real systems that couple hydrology with weathering. Nonetheless, some researchers have used the simulator TOUGHREACT (Xu & Pruess, 2001) and have chosen the dual-porosity approximation to perform reactive transport analyses of fractured systems.

A review of other models of fractured systems as of 2005 describes how processes in fractures and matrices can be treated separately (MacQuarrie & Mayer, 2005). For example, models that include a single vertical fracture or fracture zone contained within a rock matrix have been considered (Spiessl et al., 2008). More recently, detailed models of heterogeneous systems were explored for a single-phase saturated fractured system (Deng & Spycher, 2019). Those researchers described pore-scale models as well as continuum scale models and compared their results to natural systems. They focused on the geochemical alteration of single fractures. Weathering processes in a square domain with heterogeneities were also investigated with detailed simulations (Pandey & Rajaram, 2016). Those authors constructed an idealized heterogeneous permeability field where they considered a reactive transport model of weathering. In that paper, they analyzed spatial variability of the rate of the weathering reaction to address the discrepancy between weathering rates inferred from laboratory and field observations. We construct another idealized heterogeneous model different from the model described by those workers (Pandey & Rajaram, 2016). Instead of focusing on the distribution of heterogeneities, here we focus on differences in weathering advance rates (that is, velocities of weathering fronts) for homogeneous and heterogeneous systems.

Previous analyses have also been used to investigate the volumetric reaction rate (Reis & Brantley, 2017) as a function of depth in the weathering zone of a fractured system in 1D. In that effort, no numerical simulations were performed but the authors presented a semi-qualitative analysis which shows exponential decay for both weathering reaction rate and front velocity with depth. Later numerical simulations (Harman & Cosans, 2019; Harman & Kim, 2019; Lebedeva & Brantley, 2020a, 2020b) also demonstrated that weathering advance rates diminished with depth.

2.1. Overview and Context of the Approach Used in This Paper

In this paper, we consider weathering of systems of fracture-bound bedrock blocks. In our conceptualization, the unweathered system consists of rock with fractures that are filled with a porous material that is chemically inert or already weathered. We consider a fully coupled hydrological and reactive transport model of weathering within such a heterogeneous domain by taking into account diffusion and advective transport at variable Darcy velocities within fractures as well as within blocks. We specifically consider whether the latter velocities, which could have much smaller magnitudes in comparison with the velocities in fractures, could still affect the bulk, overall weathering advance rate. Our approach differs from previous approaches that separate the hydrological and reactive transport models for processes within blocks and fractures (for example, Steefel & Lichtner, 1994, 1998b, 1998a). Our approach also differs from previous work that focused only on single fractures (Deng & Spycher, 2019) in that we target systems of fractured hillsides for simulation.

The modeling we present here is based on our previous use of a 2D model of reactive transport (reaction+diffusion+advection) to explore weathering of fractured hills under water-saturated conditions. In that model we used a homogenization approach and constrained solute advection to be unidirectional at a constant Darcy velocity (Lebedeva & Brantley, 2017). Unlike other models in the literature where processes within the blocks and fractures were considered separately, we modeled a heterogeneous domain where different material properties were assumed for different parts of the fractured system. Our simulations of weathering of blocks subtended by vertical + horizonal fractures revealed features of weathering that differ substantively from weathering of parallel slabs / fractures as described in the literature (Spiessl et al., 2008; Steefel & Lichtner, 1994, 1998a). By building an additional exact model, we showed that the homogenized model satisfactorily approximates the exact model while also allowing easy and fast completion of simulations for eroding systems of blocks (Lebedeva & Brantley, 2017). We also partially corroborated our weathering-block model by comparison to measured size distributions of corestones (unweathered blocks of rock) formed during weathering.

One important observation from the homogenized model was that the weathering advance rate is inversely proportional to the volume fraction of blocks. However, flow in the subsurface in natural systems usually consists of both vertical and lateral flow (see, for example, Harman & Cosans, 2019; Harman & Kim, 2019; White et al., 2019). Lebedeva & Brantley (2017) did not explore such 2D flow because aspects of that homogenized model are not strictly correct for all cases of variable Darcy velocities. For the current paper, we nonetheless tested the homogenization approach for weathering columns (2D) and hillsides (2D) to explore the effect of variable flow though fractured systems. Again, like our previous paper (Lebedeva & Brantley, 2017), we considered a geometry for fractured rock which has generally been considered as a reasonable approximation for natural systems (Loope et al., 2020; Pollard & Aydin, 1988), namely, regular structures of joints that subtend blocks of rock matrix. We discovered that the simulations using the homogenized model approximate more exact and detailed simulations under some conditions. Those tests and the conditions of applicability of the homogenized model are summarized in Supplementary Information (SI) of this paper.

We next applied the homogenized model to systems that meet the conditions of applicability and explored the effect of 2D water flow and erosion on weathering. Given the many variables and conditions that we explore, we organized the paper into two main sections (followed by conclusions). In the first section, we simulate non-eroding hillsides under saturated and unsaturated conditions and emphasize answers to the three questions summarized in the Introduction. In the second major section, we address aspects of coupling between weathering and water flow for eroding hillsides under unsaturated condition.

3. Simulations of non-eroding Hillslopes with 2D flow

In this section we model weathering of blocks embedded in a hillslope as shown in figure S1B in Supplementary Information (SI). The blocks are shown as blue squares and the inert material as red background. Initially, all of the blocks are equal in dimension. Details of the model are considered in SI. Here we explain only some variables and parameters needed to describe the results of the simulations. We present figures to answer the three questions summarized in the Introduction, and to demonstrate the applicability of the homogenized model. We refer to the model as a simplified macro-model where we use the term “macro” because the model describes the larger-scale domain of the hillside (~100 m). The hill is in turn comprised of weathering blocks which are the small elements of the structure. The macro-model is a result of homogenization of the mesoscale model considered at the scale of ~ 0.01m –10 m. The mesoscopic description explicitly models flow within fractures and matrix. The mesoscale equations result from averaging the microscale (pore-scale~ 10 –1000 µm) equations which we do not analyze here.

Both the meso- and macroscale models are presented by the fully coupled system of hydrological and reactive transport equations which describe both saturated and unsaturated zones within blocks and joints. Advective transport in the geochemical model is determined by the variable horizontal and vertical Darcy velocities (m/s), $q_{x}$ and $q_{y}$, respectively. They are defined as follows:

$$q_{x} = - K(\psi,\phi)\frac{\partial h}{\partial x}\ ,\ q_{y} = - K(\psi,\phi)\frac{\partial h}{\partial y}\tag{1}$$

where K (m/s) is the hydraulic conductivity, h(m) and ψ(m) are hydraulic and pressure heads, respectively, $h = \psi + y$ , $\phi$ is porosity, x and y are the spatial coordinates (in m). Both porosity and pressure head change with time, t (s or y), and position during weathering, and the hydraulic conductivity can vary significantly in the vertical and horizontal planes. For the sake of simplicity, we do not include the cross terms for the conductivity tensor.

Variables $q_{x}$ and $q_{y}$ are calculated as the solution of the hydrological model coupled with the geochemical problem. The coupling occurs due to variable porosity. The latter is determined by the reactive transport model and can change drastically at the weathering front (the spatial interval across which a mineral weathers). The geochemical treatment (that is the reactive transport model plus the multicomponent scheme used to simplify the model) is a simplified version of our previous multicomponent reactive transport model developed in 1D (Lebedeva et al., 2007) and explored for several systems (Lebedeva et al., 2010; Lebedeva & Brantley, 2017, 2020b). The model describes albite dissolution and precipitation of kaolinite within blocks in the presence of an inert mineral, quartz (see SI). By focusing on this reaction, we are emphasizing weathering of feldspar, the most abundant mineral in the crust (Brantley & White, 2009). We focus on albite but we consider it just as an example of any abundant rock-forming mineral that reacts relatively quickly with pore fluids. According to (eq S19), porosity is a function of the extent of reaction, η:

$$\phi = \phi_{init} + \eta\phi_{ab}^{0}\left( 1 - 0.5\frac{\overline{V_{kao}^{0}}}{\overline{V_{ab}^{0}}} \right)\tag{2}$$

where $\phi_{init} = 1 - \phi_{in} - \phi_{ab}^{0}$ , $\phi_{in}$is the volume fraction of the inert material, $\phi_{ab}^{0}$ is the initial volume fraction of albite in rock (we assume kaolinite is not present initially within blocks), $\overline{V_{kao}^{0}}$and $\overline{V_{ab}^{0}}$(m³/mol) are specific volumes of kaolinite and albite, respectively, and the extent of reaction, η, is defined as follows:

$$\eta = 1 - \frac{Q}{Q^{0}} = 1 - \phi_{ab}/\phi_{ab}^{0}\tag{3}$$

Here Q(mol/m³) and $Q^{0}$ are the concentrations of albite in the weathering material and in bedrock, respectively; $\phi_{ab} = Q\overline{V_{ab}^{0}}$ is the volume fraction of albite in the rock.

We incorporate the reaction rate, j, as described in our previous work (Lebedeva et al., 2007, 2010):

$$j = k(1 - \eta)(C^{e} - C)\tag{4}$$

Here k (s^-1) is an effective rate constant (see SI), C (mol/m³) is the concentration of a species in pore fluid,$C^{e}$ is the concentration of this species in porefluid in equilibrium with albite and kaolinite. In the reactive transport model for the combined unsaturated-saturated flow, the kinetic function j is multiplied by water saturation of the porosity, $\theta_{s}$. This term is the ratio of the volume of water present in a heterogeneous media relative to the volume of pores (see SI). This follows from the general principles of averaging and homogenization of microscale equations (Hornung, 1997; Molins & Knabner, 2019). In the case of solid, gas, and fluid phases, the new effective kinetic constant $k\theta_{s}$ is directly proportional to the specific reactive surface area. We can express saturation of pores with water as follows (see SI):

$$\theta_{s} = \frac{\theta}{\phi}\tag{5}$$

where $\theta$ is the fraction of the weathering volume filled with water (volumetric water content). When the pores are saturated $\theta = \phi$, $\theta_{s} = 1$ and the effective kinetic constant is equal to that for the case of saturated flow.

Solving the mesoscale model equations, we obtain the time evolution of the variables h, C, $\phi$ and η in the spatial domain of interest. The simplified macro-model that we obtained previously (Lebedeva & Brantley, 2017) has a similar form to the mesoscale model. But unlike the variables in the mesoscale model which relate either to blocks or to fractures (depending on coordinates) the variables of the macro-model describe a new homogenized domain at each point. So, these variables are averaged over the unit cell (fig. S1). The volume of this cell consists of the volume of the block, $\left| \Omega_{B} \right|$, and the volume of the weathered inert material $\left| \Omega_{F} \right|$. Therefore, if the initial value of the extent of reaction is equal to zero within the blocks, and equal to unity between the blocks, then the initial value of the averaged extent of reaction, $\eta_{av}(x,y,0)$, is equal to $\phi_{F}$which is the volume fraction of fractures in the rock (see SI):

$$\small{ \eta_{av}(x,y,0) = \frac{\left| \Omega_{F} \right|}{|\Omega|} = \phi_{F}, |\Omega| = \left| \Omega_{B} \right| + \left| \Omega_{F} \right| \tag{6} }$$

In the model, the initial volume fraction of fractures is constant with respect to space, $\phi_{F}(x,y,0) = const$, for the structure depicted in figure S1. For exploration of variable fracture density, we simulate a system that is described by a variable initial extent of reaction,$\ \eta_{av}(x,y,0) = \phi_{F}(x,y,0)$. Here, fracture density is defined as the volume fraction of fractures in the rock, regardless of orientation. With this definition it is directly proportional to fracture density as defined in the geotechnical literature, that is, the number of fractures per unit of length.

We consider a 2D domain (x,y) under a hill surface with the following boundaries (fig. S2): y=H(x) at $0 \leq x \leq L$; $0 \leq y \leq H(0)$ at x=0; $0 \leq y \leq H(L)$ at x=L; $0 \leq x \leq L\ at\ y = 0$ where the hill surface is defined by$\ y = H(x)$. Here, L is the horizontal distance drawn at the base of the hill from the ridge crest to the channel. We consider the hill slope with the following hydraulic boundary conditions: no-flow boundary conditions at the boundaries $x = 0,\ 0 \leq y \leq H(0)$ and $0 \leq x \leq L$, y=0. A specified head condition is applied to the right boundary to allow flux out of the system:

$$h = h_{L}\ at\ x = L,\ 0 \leq y \leq H(L)\tag{7}$$

Finally, the fluid influx directed along the unit normal n to the hill surface $y = H(x)$ is specified at this surface:

$$K\left. \ \frac{\partial h}{\partial n} \right|_{y = H(x)} = F_{0}\cos{\vartheta(x)}\tag{8}$$

where $F_{0}$(m/s, m/y) is the vertical rate of infiltration at the surface, and $\vartheta$ is the hill slope angle, $\cos\vartheta = {(1 + \left( \frac{dH}{dx} \right)^{2})}^{- 0.5}$ .

We assume that the species in the pore fluids within the hill are initially in equilibrium with albite and kaolinite: at $t = 0\ C = C^{e}$. The boundary conditions for the concentration of the dissolved species, C, are the same as we have considered previously (Lebedeva & Brantley, 2013). Specifically, for the left and right boundaries as well as at the bottom of the hill, the concentration gradients for the species in the porefluid are set equal to zero. We assume that the solute concentrations in fluids before they infiltrate into the column are uniform, constant in time, and equal to some average value $C^{R}$at the top of the hillslope. This boundary condition at the upper boundary determines the solute concentrations at the regolith surface everywhere along the hill surface at $y = H(x),0 \leq x \leq L:\ C(x,y,t) = C^{R}$. Reaction occurs because $C^{R} \neq C^{e}$.

To address the questions in the Introduction, we performed simulations using COMSOL Multiphysics software (COMSOL, 2008), a software platform that enables interactive modeling of a variety of physics-based problems using advanced numerical methods and is especially useful in handling coupling between different systems. Simulations were performed for the dimensionless model (see SI). For each of the questions, we typically first demonstrate the success of the homogenized model.

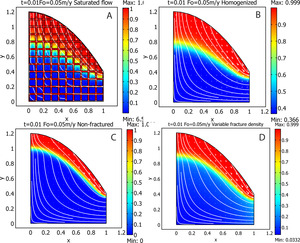
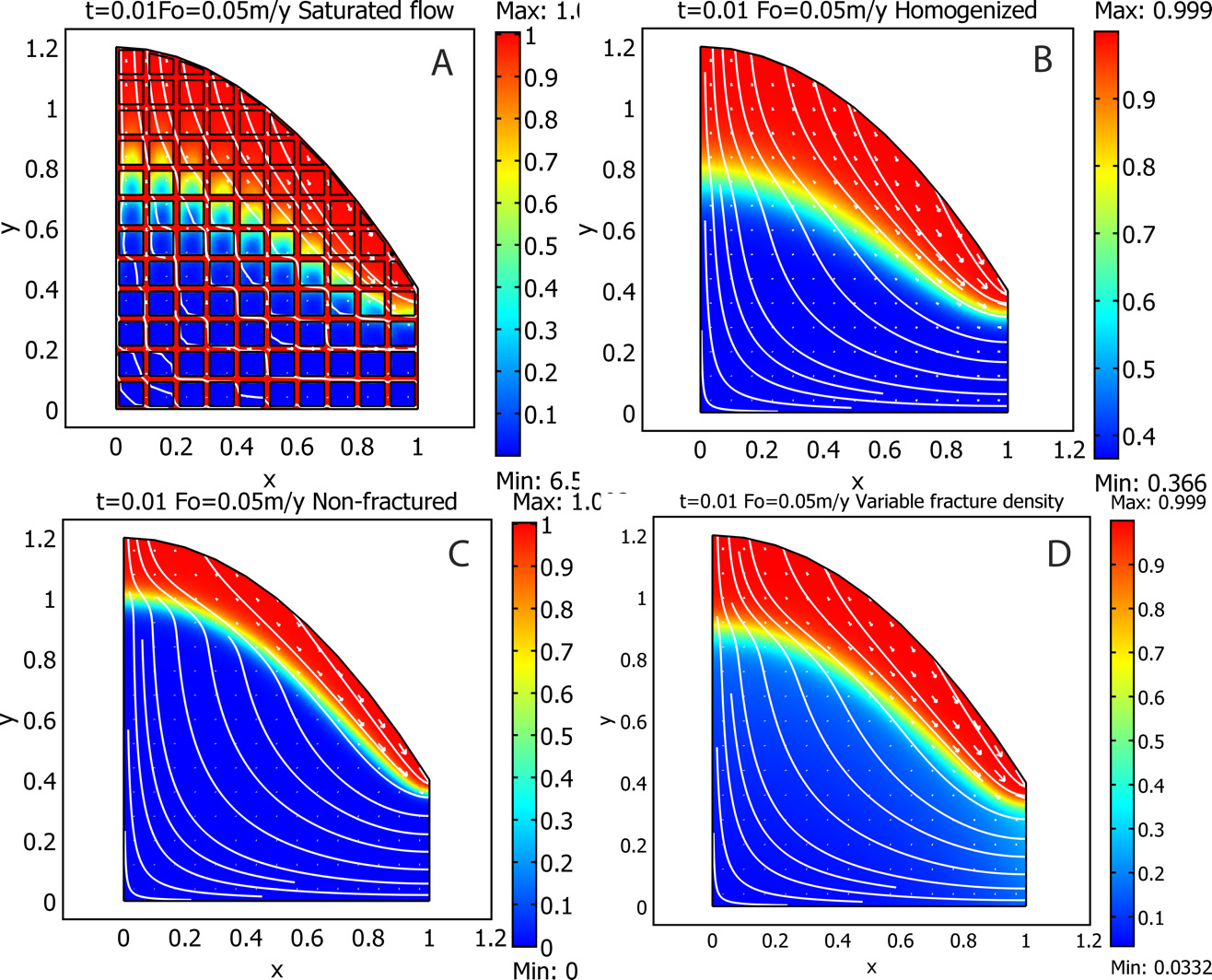
3.1. Question One: How Does Fracture Density Affect Weathering Depth?

With figures 1A and B and figures S3 and S4 in SI, we document that simulations of weathering fractured hillslopes using the simplified homogenized model satisfactorily approximate the solution for the exact model for the case of saturated subsurface flow. From this we infer that we also can use the homogenized model to simulate systems for variable fracture density.

Figure 1.Simulations for a fractured non-eroding hillslope for the case of saturated flow at $t = 3.2 \times 10^{6\ }y$.

The extent of reaction $\eta$ is shown by increasingly warm colors from blue (bedrock) to darkest red (100% depletion of albite in weathered material). Squares outlined in black indicate the initial unfractured rock blocks separated by fractures containing inert material. (A) Mesoscale (exact) solution. (B) Solution using the homogenized model to approximate the exact solution. (C) Mesoscale (exact) solution for the non-fractured hill. (D) Homogenized model applied to the case where density of fractures diminishes with depth according to the equation $\phi_{F} = 0.366e^{2(y - H(x))}$. For (D) the regolith is not as thick as for the case with uniform distribution of fractures at $\phi_{F} = 0.366$ (as shown in (A) and (B)) but it is greater than for the non-fractured hill (fig. 1C). The white lines depict the streamlines; the white arrows are proportional to the Darcy velocities. Parameters are: $F_{0} = 0.05\ m/y$ , $k = 3.25 \times 10^{- 9}s^{- 1}$, $K = 10^{- 5}\phi^{3}m/s$, L=20 m, $D = 8 \times 10^{- 10}m^{2}/s$; $Q^{0} = 4 \times 10^{3}mol/m^{3}$,$C^{e} = 0.2\ mol/m^{3}$, $C^{R} = 0$, $\overline{V_{ab}^{0}} = 10^{- 4\ }m^{3}/mol$, $\overline{V_{kao}^{0}} = 9.934 \times 10^{- 5}m^{3}/mol$,${\ \phi}_{ab}^{0} = 0.4$, $\phi_{init} = 0.1$. The dimensionless equation for the hillslope is as follows: $H(x) = - 0.8x^{2}$+1.2.

In figure 1, we compare simulated regolith for the hillslope as a function of fracture density. Figure 1D demonstrates that when the (open) fracture density diminishes with depth, as has been postulated in the literature for exhumed rock systems and observed in the field (Clarke & Burbank, 2011), the calculated regolith thickness is less than for the case of a depth-independent fracture density as shown in figures 1A and B. The fracture density is the same at the hill surface in figures 1A and D. Figure 1C documents that the weathering advance rate is smaller for unfractured rocks in comparison to the fractured structures at the same conditions.

3.2. Question Two: How Does Lateral Flow Affect Weathering Depth?

Our next step was to analyze the weathering advance rate for fractured systems in the presence of lateral flow. In this section we illustrate our analysis with figure 2. Figure 2 shows a weathering, non-eroding hill where flow is unsaturated near the land surface (that is, the vadose zone) under the hill surface. Figures 2A and C demonstrate that the simple homogenized model also satisfactorily approximates the exact solution, although the approximation is not as good as for the case of saturated flow (compare figures S3 and S5 in SI). This is expected because the kinetic constant k is multiplied by saturation for the case of unsaturated flow (eqs 4, 5, S6, and S7) and the approximation by the homogenized model is better for larger kinetic constants (Lebedeva & Brantley, 2017). Saturation is less than unity for unsaturated flow when wetness, $\theta$, is less than porosity, $\phi$. This also explains why the weathering front is wider for the case of unsaturated flow (fig. 2B and D): the thickness of the weathering front is directly proportional to$({k\theta_{s}\ )}^{- 1}$ (Lichtner, 1988). Figure S5 compares profiles of solute concentrations and extents of reaction for the exact, homogenized and non-fractured solutions at various distances (along x) from the ridgetop. The figure documents that the approximation becomes more accurate at larger values of x.

Figure 2.A comparison of the exact solution (A) and (B) to the homogenized solution (C) and (D) for a fractured but non-eroding hillside.

Also shown are the solutions for a non-fractured hill of the same geometry (E) and (F). All examples were simulated under unsaturated flow at $t = 3.2 \times 10^{6\ }y$. Water table is shown by the black curve. The white lines depict the streamlines, the white arrows are proportional to the Darcy velocities. Figures 2A, C, and E show the extent of reaction, η (eq 3)(by color which changes from blue to red with η increase); figures 2B, D, and F present the dimensionless (see SI) reaction rate j (eq 4) multiplied by $\theta_{s}$ (eq 5). Parameters are: $F_{0} = 0.05\ m/y$ , $k = 7.5 \times 10^{- 9}s^{- 1}$, $K = 10^{- 5}\phi^{3}m/s$, L=20 m, $D = 8 \times 10^{- 10}m^{2}/s$; $Q^{0} = 4 \times 10^{3}mol/m^{3}$,$C^{e} = 0.2\ mol/m^{3}$, $C^{R} = 0$, $\overline{V_{ab}^{0}} = 10^{- 4\ }m^{3}/mol$, $\overline{V_{kao}^{0}} = 9.934 \times 10^{- 5}m^{3}/mol$,${\ \phi}_{ab}^{0} = 0.4$, $\phi_{init} = 0.1$, $\phi_{F} = 0.366$.
The dimensionless equation describing the geometry of the hillslope is as follows: $H(x) = - 0.8x^{2}$+1.2.

We have previously shown that ignoring fractures underestimates the weathering advance rate (Lebedeva & Brantley, 2017). In that work, however, we focused only on cases with unidirectional constant downward advection. For that case, the weathering advance rate for fractured systems, W, can be calculated as follows

$$W = \frac{W_{0}}{\phi_{B}}\ ,\ \ \phi_{B} = \frac{\left| \Omega_{B} \right|}{|\Omega|}\tag{9}$$

where $W_{0}$ is the weathering advance rate for non-fractured system, $\phi_{B} < 1$ is the volume fraction of blocks, $|\Omega| = \left| \Omega_{B} \right| + \left| \Omega_{F} \right|$ is the total volume of a weathering column. Our simulations here document that, at least under some conditions, (eq 9) holds also for the case of 2D flow, that is vertical+horizontal flow at variable Darcy velocities.

As shown multiple times in the literature (Lebedeva et al., 2010), the weathering advance rate for non-fractured system in the case of unidirectional advection at the constant Darcy velocity $q_{y}$ is calculated by the following equation:

$$W_{0} = \frac{(C^{e} - C^{R})q_{y}}{Q^{0}}\tag{10}$$

(for example, Ortoleva et al., 1987). This equation or versions of it are commonly used by geochemists in treating weathering (Brantley & White, 2009). But this equation is not correct in the presence of lateral flow. In this case the weathering advance rate must be calculated with a different equation as published previously (Lebedeva & Brantley, 2020a). We reproduce the equation here after correction for fractured systems:

$$\scriptsize{ \begin{align} W_{av}(t) &= \frac{1}{L}\int_{0}^{L}{W(x,t)dx} \\ &= \frac{1}{\phi_{B}Q^{0}L}\biggl\{ \int_{H(x)}\biggl( - D\phi\frac{\partial C}{\partial y}dx + D\phi\frac{\partial C}{\partial x}dy \biggr) + \int_{0}^{H_{L}}{{(q_{x}C)}_{x = L}dy} \biggr\} \tag{11} \end{align} }$$

Here $W_{av}$ is the vertical component of the weathering advance rate averaged over the width of the weathering hill L, H(x) is the y-coordinate of the surface of the hill, and H_L is the width of the outlet channel (fig. S2). This channel dimension is the vertical thickness of the zone of water flow into the stream or valley. It was shown previously (Lebedeva & Brantley, 2020a) that when the concentration gradients at the surface are small, the following relationship holds:

$$\begin{align} W_{av}(t) &= \frac{1}{L\phi_{B}Q^{0}}\iint_{\Omega}^{}{j(x,y)\theta_{s}dxdy} \\ &= \frac{1}{L\phi_{B}Q^{0}}\int_{0}^{H_{L}}{{(q_{x}C)}_{x = L}dy} \tag{12} \end{align}$$

(Again, here, we modified the earlier result for fractured systems). Thus, the weathering advance rate could be calculated either using the solute discharge at the outlet of the system (at x=L) or using the weathering rate j. The latter method probably cannot be used in practice to estimate weathering advance rate but equation (12) could be used to calculate chemical weathering rates (Lebedeva & Brantley, 2020a). Versions of this idea have been explored repeatedly, for example (Pačes, 1983; Velbel, 1993). Figure S6 shows that (eq 12) satisfactorily fits the simulations shown in (fig. 2A and C), that is $W_{R\ av}(t) = W_{Flux\ av}(t)$ where $W_{R\ av}(t)$ is the weathering advance rate as expressed by

$$\begin{align} W_{R\ av}(t) &= \frac{I_{R}(t)}{LQ^{0}\phi_{B}}, \\I_{R}(t) &= \iint_{\Omega}^{}{j(x,y)\theta_{s}dxdy} \tag{13} \end{align}$$

and $W_{Flux\ av}(t)$ is the weathering advance rate determined from the weathering flux

$$\begin{align} W_{Flux\ av}(t) &= \frac{I_{F}(t)}{LQ^{0}\phi_{B}} , \\ I_{F}(t) &= \int_{0}^{H_{L}}{{(q_{x}C)}_{x = L}dy} \tag{14} \end{align}$$

Equation (14) also emphasizes that the weathering advance rate diminishes with increasing time (fig. S6).This phenomenon, where the inclusion of lateral flow causes weathering advance rate to decrease with depth has also been discussed by others in the literature (Harman & Cosans, 2019; Reis & Brantley, 2019).

Equation (9), describing the relationship between weathering advance rates for fractured and non-fractured systems, can be used to constrain volume fractions of fractures and the ratios of the fracture apertures, d, to fracture spacing, δ. According to (eq 9), the relationship between the weathering advance rates for the fractured hill, $W_{fr}$, and the non-fractured hill, $W_{nfr}$, near the ridge top is described as follows

$$W_{fr} = \frac{W_{nfr}}{\phi_{B}}\tag{15}$$

For the time-dependent weathering advance rate, we define the regolith thickness, $h_{reg}$, as

$$h_{reg} = \int_{0}^{T}{W(t)dt}\tag{16}$$

where t=T is the cumulative (total) time duration of weathering. With (eqs 15 and 16), it follows that

$$\frac{h_{reg\ fr}}{h_{reg\ nfr}}\ = \phi_{B}^{- 1} = \frac{|\Omega|}{\left| \Omega_{B} \right|}\tag{17}$$

where $h_{reg\ fr}$and $h_{reg\ nfr}$ are the thicknesses of regolith for fractured and non-fractured systems, respectively. If δ is the fracture spacing, that is, the size of the square in (fig. 2A), and d is the fracture aperture, that is, the distance between squares then $|\Omega| = \left| \Omega_{B} \right|{(1 + \frac{d}{\delta})}^{2}$ (Lebedeva & Brantley, 2017). Thus, it follows from (eq 17) that

$$\frac{d}{\delta} = \sqrt{\frac{h_{reg\ fr}}{h_{reg\ nfr}}} - 1\tag{18}$$

Relationships (17) and (18) yield insights into the depth of weathering as a function of fracture density, fracture spacing and aperture.

Figure 2A shows a comparison of the fractured system and the non-fractured system (fig. 2E) simulated for the same parameters. Using figures 2A and E we can estimate the ratio of fracture aperture to fracture spacing by comparison of regolith thicknesses at the ridgetop for fractured and non-fractured hills:

$$\frac{d}{\delta} = \sqrt{\frac{h_{reg\ fr}}{h_{reg\ nfr}}} - 1 \approx \sqrt{\frac{0.45}{0.3}} - 1 = 0.22.$$

We can also show the applicability of the homogenized model by comparing the weathering advance rates calculated using (eqs 13 and 14). Figure S6 documents that the homogenized model satisfactorily approximates the exact model (for example, dimensionless$\ I_{R}(0.01) = 21.9$ for the exact solution while $I_{R}(0.01) = 20.7$ for the homogenized solution). Figure S6 also demonstrates that the weathering advance rate for the non-fractured hill is less than for the fractured hill as long as the other parameters are maintained the same ($I_{R}(0.01) = 16.0$).

Finally, we could also estimate the average regolith thickness under the hill surface for the time interval [0,T] (eq 16) using the average weathering advance rate and equations (13) and (14). Alternately, the average regolith thickness could be estimated from the change of the total mass of albite during weathering according to the following equation (see SI for derivation):

$$\small{ h_{reg\ fr} = \frac{\left| \Omega_{B} \right|}{L(\eta(H,T) - \eta(0,T))} \cdot \frac{M(0) - M(T)}{M(0)} \tag{19} }$$

where for t=T or t=0, M(t) is the mass of albite within the hill:

$$\begin{align} M(t) &= \int_{\Omega}^{}{Q(x,y,t)d\Omega}, \eta(H,t) \\ &= \frac{1}{L}\int_{0}^{L}{\eta\left( x,H(x),t \right)dx}, \eta(0,t) \\ &= \frac{1}{L}\int_{0}^{L}{\eta(x,0,t)dx} \tag{20} \end{align}$$

3.3. Question Three: How Do Weathering and Fractures Affect the Water Table?

We investigated the relationship between weathering and the water table for unfractured systems previously (Lebedeva & Brantley, 2020b). We found that the water table locates deeper for a weathered (as compared to unweathered) system as long as i) other conditions and parameters are held the same, and ii) the hydraulic conductivity of the weathering zone is larger than the hydraulic conductivity of protolith. The deeper water table is expected if connected porosity increases during weathering. From the simulations completed here, the water table also locates deeper for fractured weathered systems in comparison with unfractured, even in the presence of 2D flow. This is because the weathering zone is larger for the fractured as compared to the unfractured hill (fig. 2).

We also explored the effect of the contrast in permeability for blocks and fractures for an inert non-weathering hill as shown in (fig. S7). Figure S7 shows that the water table is located deeper for a non-weathering hill when the hydraulic conductivity of fractures is greater than blocks (as expected) in comparison with the case when hydraulic conductivity is homogeneous within the hill. When blocks start to weather this effect increases.

4. Weathering of eroding, fractured Hillslopes with 2D flow

With the simplified homogenized model, we now can also analyze fractured hills that are both weathering and eroding. To model an eroding weathering hill, we use essentially the same model formulation as we just described, but we assume that the hill surface lowers at a constant vertical rate E by introducing the moving system of coordinates (see Appendix in Lebedeva & Brantley, 2013):

$$\overline{y} = y + Et,\ \ \overline{t} = t\tag{21}$$

Exploring the evolution of the hills through simulations, we observe that the transient solutions reach a dynamical equilibrium. This steady state is characterized by a regolith thickness that remains constant in time. For such a steady-state hill, the vertical component of the weathering advance rate equals the vertical component of the erosion rate E.

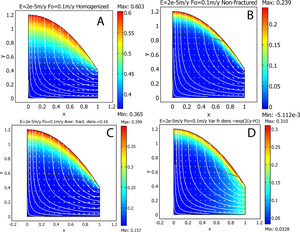
Figure 3 shows fractured and unfractured weathering hills simulated at a constant vertical erosion rate, $E = 2 \times 10^{- 5}$ m/y, and infiltration flux at the hill surface, $F_{0} = 0.1\ m/y$. The simulations are shown after the hills attained a dynamical steady state where weathering advance rate equals erosion rate. All hills are shown to be weathering in the weathering regime where reaction kinetics are rate-limiting. For this case, the weathering profile is incompletely developed, that is, the extent of reaction is less than unity at the land surface, and the rate of weathering depends upon the reaction rate constant (Lebedeva & Brantley, 2013). However, the thickness of regolith (the weathered zone) and the extent of reaction at the surface are larger for the fractured than the unfractured hill (0.6 versus 0.2 in figures 3A and B). The water table is also located deeper under the surface of the fractured hill. When the infiltration flux at the surface, $F_{0}$, is increased, the weathering regime approaches the transport-limited regime. For example, figure S8 shows that at $F_{0}$= 0.5 m/y the simulation approaches the transport-limited regime for the fractured system. In this regime, the extent of reaction tends to unity at the surface (the profile becomes completely developed) and the rate of weathering eventually shows no dependence on the reaction rate constant. In contrast, for those same conditions of increased infiltration, the non-fractured hill still weathers in the weathering-limited regime (figures S8C and D). Note that at this value of surface influx F_o, the flow within the non-fractured hill has become saturated. Figures 3A and S8A show that the water table for the fractured hill becomes shallower as surface influx increases.

Figure 3A depicts simulations for a pre-existing jointed rock structure, that is, the rock is previously jointed at all depths with constant joint spacing. This likely pertains to some natural systems where faulting is controlled by factors unrelated to exhumation or weathering. For some systems it might be more likely that new joints could be continuously forming at the bottom of the column, perhaps in response to exhumation. This is an important question because many workers argue that weathering is affected as fractures open during rock exhumation (St. Clair et al., 2015; Wang et al., 2021).

Figure 3.Comparison of weathering and eroding hills that are characterized by a constant fracture density (A), no fractures, (B), or variable fracture density (C and D).

Extent of reaction is shown by color (note that scales are different in the panels). The fractured hills were simulated using the homogenized model. The initial value of the extent of reaction is equal to $\phi_{F} = 0.366$ within the entire domain for the fractured model (A) or 0 for the unfractured model (B). Panel (C) shows simulations at $\eta(x,y,0) = \phi_{av} = 0.16$ as calculated by averaging the variable fracture density${\ \phi}_{F} = 0.366e^{2(y - H(x))}$. The latter is used for simulations shown in panel (D). Parameters are: $E = 2 \times 10^{- 5}m/y$, $F_{0} = 0.1\ m/y$ , $k = 7.5 \times 10^{- 9}s^{- 1}$, and saturated $K = 10^{- 5}\phi^{3}m/s$. The black curve depicts the water table.

Here we have not modeled a mechanism for jointing and do not consider feedback to couple the fracturing, erosion, and weathering. Nonetheless, we can show the effect of variable fracture density (fig. 3C and D). As assumed in the previous simulation (fig. 1D), we assume here that the fracture density diminishes with depth according to the equation $\phi_{F} = 0.366e^{2(y - H(x))}$ . We show two scenarios. Figure 3C illustrates simulations for the case when such a variable pattern in fracture density forms continuously. For this case we simulate weathering and erosion for an averaged value of fracture density calculated as, $\phi_{av} = \eta_{av}(x,y,0) = |\Omega|^{- 1}\int_{\Omega}^{}{0.366e^{2\left( y - H(x) \right)}d\Omega} = 0.16$. As expected, the regolith thickness and the extent of reaction at the hill surface are less than in the case of a constant fracture density equal to 0.366 (fig. 3A). The second scenario shows weathering and erosion when a pre-existing fractured structure does not change with time (fig. 3D). In this case erosion removes the upper more fractured layers, and as time elapses, this means that weathering proceeds within a domain which now has a lower fracture density. The result is thinner regolith and a lower extent of reaction at the hill surface.

For simulations made for weathering of a hill in the presence of erosion, the weathering advance rate attains a constant value equal to the erosion rate after a suitable time interval. The value of the time interval increases as the erosion rate decreases. Figure 4 shows the functions $I_{R}(t)$ and $I_{F}(t)$ (eqs 13 and 14). In the presence of erosion with a constant vertical rate E, equation (A7) in the moving system of coordinates takes the form:

$$\frac{\partial\eta}{\partial\overline{t}} + E\frac{\partial\eta}{\partial\overline{y}} = \frac{j\theta_{s}}{Q^{0}}\tag{22}$$

For the steady state when $(\frac{\partial\eta}{\partial\overline{t}}) = 0$, we obtain by integration:

$$\small{ E = \frac{1}{LQ^{0}(\eta(H,T) - \eta(0,T))}\int_{\Omega}^{}{j\theta_{s}d\Omega} \tag{23} }$$

where η(H,T) and η(0,T) are the averaged extent of reaction at the hill surface y=H(x) and at the bottom of the hill y=0, respectively (eq 20), for a steady state as defined by some sufficiently long time period [0,T]. Here we assume that T is the time when the hill attained a steady state. Note that η(0,T) = 0 for non-fractured hills. But for the homogenized model for a variable fracture density $\eta(x,0,T) = \phi_{F}(x,0,T)$ is a function of x, so η(0,T) is its averaged value.

Figure 4.Dimensionless functions $I_{R}(t)$ (A)(eq 13) and${\ I}_{F}(t)$ (B)(eq 14).

At $T \approx 0.0035$ the system reaches the steady state. Parameters are as in fig. S8.

When the hilltop weathers in the regime close to the transport-limited regime, that is when $\eta(H,T) \approx 1$, and the rate of weathering is not dictated by reaction kinetics, we can use (eq 18) to estimate the ratio of fracture aperture to fracture spacing. Using (fig. S8) we obtain:

$$\frac{d}{\delta} = \sqrt{\frac{h_{reg\ fr}}{h_{reg\ nfr}}} - 1 \approx \sqrt{\frac{1.1}{0.7}} - 1 = 0.25$$

which corresponds with the geometry presented in (fig. 2).

Thus, in the presence of erosion, fracturing leads to an increase in both the steady-state regolith thickness and the extent of reaction at the hill surface. The weathering advance rate tends with time to the erosion rate. The position of the water table is deeper in the presence of fractures, but the position of the water tables is shallower for water influxes at the land surface that are larger. Note that for unfractured as well as for fractured systems the position of the water table becomes deeper in comparison with unweathered systems. But an increase in the thickness of the weathered zone in the presence of fractures is an additional factor moving the water table deeper.

5. CONCLUSIONS

We have little ability to quantitatively predict the depth of weathered material (soil) from location to location. This is surprising given the importance of soil to human society and how fast it is currently eroding worldwide (Wilkinson & McElroy, 2007). Much of our intuition about what controls weathering is based on simple conceptual models that are easy to explore as thought experiments. But, as shown by many researchers previously, and as shown in this paper, many factors affect weathering advance from location to location. Clearly, numerical models are needed that can simulate regolith development accurately and that can take into account important soil-forming factors. Perhaps the most successful models of water-rock interaction (including weathering) are reactive transport models. These models were first used to consider homogeneous porous media where reactive transport generally occurs by advection and diffusion. Much of our intuition about weathering and erosion is substantiated by numerical reactive transport models.

However, geologic media is not homogeneous, and when inhomogeneities are included in reactive transport models, simple conceptual models are less successful in making predictions. When researchers first used reactive transport models to consider fractures, they usually assumed that transport into the matrix between fractures only occurs by diffusion while advective transport was limited to fractures. A few modelers used dual-porosity models to treat fractured media. In real systems, advective transport also occurs within the matrix, but with much slower velocities than in the fractures. So, models neglecting advective processes in rock matrix can be inaccurate.

To address this problem, we developed 2D simulations from models which take into account both diffusion and advective transport within heterogeneous media consisting of blocks and fractures. In our simulations, the Darcy velocities are variable in space and time and respond to weathering within the matrix (inside blocks). In turn, the flow affects weathering. We performed simulations for weathering hills that are either eroding or not eroding, and are under conditions of saturated or unsaturated flow.

To increase the utility of the modeling effort, we developed a simplified homogenized model and compared it to the exact models considered here. The accuracy of approximation depends on the ratio of the characteristic length of one block and adjacent fractures, ℓ, to the column length, L, the parameter ε=ℓ/L<<1. For our model, the applicability essentially depends also on the magnitudes of the Darcy velocities which are determined by the influx of the solute at the inlet of the system, $F_{0}$, as well as on flow regimes. An additional utility of homogenization is that it exemplifies how to develop appropriate simplified models for systems with heterogeneities such as fractures. As such, our homogenization approach teaches concepts of weathered systems – perhaps even more than other more accurate numerical models.

Where the homogenized model is applicable, we simulated weathering of columns (see SI), non-eroding hills with variable fracture density, and eroding hills. Our simulations document that the weathering advance rate in the presence of fractures is larger than for similar non-fractured systems when all other parameters and conditions are held the same. The average values of regolith thickness for fractured systems are a function of the ratio of fracture aperture to fracture spacing. Simulations also show that larger weathering advance rates correlate with increasing fracture density. This is the answer to the first question which we posed at the beginning of the paper: weathering advance rate increases with fracture density.

Our second question was how does flow regime affect weathering advance rate? The simulations show that for systems with 2D flow (where lateral flow of water decreases the average vertical infiltration rate), the weathering advance rate is slower than for the case of quasi-vertical flow.

Finally, when our hill simulations are set up to include an unsaturated zone, they show that fracturing affects the location of the water table. For weathering systems, the water table locates deeper for fractured as compared to unfractured systems under the same sets of parameters and conditions.

The use of exact and homogenized reactive transport models can build intuition on the part of geochemists in how natural systems work and how to conceptualize them. Only with such efforts will we learn to predict how soil depths vary across landscapes.

ACKNOWLEDGMENTS

Funding is acknowledged from DOE OBES DE-FG02-05ER15675 and from the Hubert and Mary Barnes Professorship Endowment Funds (Penn State) to SLB. The authors also appreciate several insightful reviews from anonymous reviewers and editorial handling of the manuscript.

AUTHORS CONTRIBUTION

M. I. Lebedeva: Conceptualization of study, formulation of models, writing of first draft of paper and revisions, and visualization of model output.

S.L. Brantley: Revisions of paper, comparison of model output with natural systems.

SUPPLEMENTARY INFORMATION

https://earth.eps.yale.edu/~ajs/SupplementaryData/2023/Lebedeva

DATA AVAILABILITY

No data are presented. Simulations were performed by COMSOL

Editor: C. Page Chamberlain, Associate Editor: Kate Maher