Large-strain Elastic and Elasto-Plastic Formulations for Host-Inclusion Systems and Their Applications in Thermobarometry and Geodynamics

1. INTRODUCTION

Between their formation and exhumation, rocks commonly experience a variety of changes in pressure and temperature (P-T) conditions. During these changes, mineral assemblages are evolving chemically as well as physically as evidenced by the minerals that are stable in various igneous and metamorphic exhumed rocks. Mineral/melt inclusions which are found in dense, high-pressure minerals from mantle xenoliths and metamorphic rocks provide direct evidence for the stable phases deep in the earth’s crust and mantle, and are commonly used as probes of the physical conditions in the deep Earth (for example, Ferrero & Angel, 2018). There is a plethora of geodynamic environments and mechanisms that lead to the complex P-T evolution of rocks and their subsequent exhumation to surface conditions (fig. 1). The processes in these geodynamic environments cause P-T changes that affect all the stable phases which occur in the Earth’s interior. During their burial and exhumation, the present phases will change their volume according to the equation of state (EOS) that determines their Pressure-Volume-Temperature (P-V-T) relation. Yet, the P-V-T behavior of different minerals can vary significantly, and the volumetric response is not the same for every mineral when pressure and temperature changes. This fact leads to the differential expansion/contraction of minerals with the concomitant development of stress/pressure gradients in the multiphase rock (Adams et al., 1975; Rosenfeld & Chase, 1961). The development of stress/pressure differences in host-inclusion systems can be documented by the estimates of residual pressure/stress in fluid/solid inclusions (Enami et al., 2007; Robin, 1974; Roedder & Bodnar, 1980) as well as by the effects of large deviatoric stresses on mineral hosts. These effects include the strain-induced birefringence, the development of dislocations and the fracturing of the host phase (Howell et al., 2010; Plümper et al., 2022; Rosenfeld, 1969; Taguchi et al., 2019; Van der Molen & Van Roermund, 1986).

Figure 1.Sketch illustrating various geodynamic environments and processes related to rock burial and exhumation.

The colored regions represent the lithosphere. The size of a volcano has been exaggerated for illustration purposes. Abbreviations: gph, graphite stability region; diam, diamond stability region. The thin dashed line shows schematically the limit where graphite and diamond coexist in the lithospheric keel (after Haggerty, 1999).

The quantitative estimation of the pressure/stress differences requires mechanical models that are based on continuum mechanics. The basis for developing such mechanical models is the accurate description of volume changes that requires an EOS for every system. However, the development of pressure variations due to differential expansivity/compressibility is not limited to the mineral scale. In principle, any host-inclusion system where materials can adjust their volume as a response to P-T changes has the potential to develop significant pressure variations (Moulas et al., 2013; Schmalholz et al., 2020; Tajčmanová et al., 2015; Vrijmoed et al., 2010). The EOS in that case is related to the multiphase system rather than a single phase (Connolly, 2009). Currently, most EOS for minerals that are used in internally consistent thermodynamic databases consider only the volumetric deformation and treat all phases as isotropic with respect to their elastic properties (Berman, 1988; Chatterjee et al., 1998; Gottschalk, 1996; Helgeson et al., 1978; Holland & Powell, 1998, 2011). Thus, it is not surprising that the most widely used models for host-inclusion deformation consider linear-elastic/isotropic rheology (Van der Molen & Van Roermund, 1986; Y. Zhang, 1998). More elaborate mechanical formulations, that consider the nonlinear EOS of minerals, still assume that the deviatoric deformation is linear elastic and the mineral phases are isotropic (Angel et al., 2017; Guiraud & Powell, 2006; Moulas et al., 2020). Such solutions seem to be sufficient for the study of pressurized mineral inclusions like in the case of quartz-in-garnet host-inclusion system (Bonazzi et al., 2019; Moulas et al., 2020; Thomas & Spear, 2018). On the contrary, the decompression of Ultrahigh Pressure (UHP) rocks and mineral inclusions that experience phase transitions can justify a large-strain, more accurate approach. This may be of particular use in the study of multiphase systems with more complex EOS which may result to significantly larger strains (for example, rocks that experience partial melting, melt inclusion deformation and relatively large pressure changes in minerals).

The examination of problems that require large strain lead to considerably more complex and both physically and geometrically non-linear mechanical expressions compared to the linear-elastic cases that are typically encountered in Earth-science applications (e.g., Bower, 2009; Horgan, 2001; Zingerman et al., 2016). By physical non-linearity we refer to the material non-linearity, i.e., the dependence of the thermo-elastic moduli on P-T conditions (e.g., Babuška et al., 1978; Milani et al., 2015). However, the observable differences in elastic properties require the consideration of a large range of pressure and/or temperature conditions. In that case, the strain that can develop during confinement may be significant. Under large strains and finite deformation, the initial and final state of materials are distinctly different and thus certain thermodynamic and geometric restrictions apply (see also Bower, 2009; Fung, 1965). Therefore, apart from material non-linearity (the change of elastic moduli in P-T), one may also need to consider the geometric non-linearity (the effects of finite strain) that would account for changes of distances between material points during large deformation.

In this work we present a new formulation for the study of spherical and isotropic host-inclusion systems (that is also known as the Lamé problem) under large strain. Our new formulation can handle the non-linear volumetric strain that develops as a result of significant P-T changes in geomaterials. As a first approximation, the deviatoric stresses are calculated using linear-elasticity theory while for the volumetric strain any EOS can be used (for example, Murnaghan, Birch-Murnaghan, Tait, et cetera). This leads to a new, non-linear analytical solution whose results can be compared to the results of a similar, but approximate, solution presented by Guiraud and Powell (2006). Our new solution is tested against numerical models that have been recently used in elastic geobarometry (Moulas et al., 2020) and we demonstrate convergence for high numerical resolutions. We show that the discrepancy between the linear and the non-linear elastic solutions is small for most barometry applications. Furthermore, we validate our approach by comparing our solutions with results from a newly-derived, fully-non-linear, elastic solution that considers the effects of large finite strain and the pressure-dependence of bulk modulus (Levin et al., 2021). Finally, we show that for the cases of very large volumetric deformations, the incorporation of plasticity can affect the elastic solutions dramatically and, can be responsible for the development of significant pressure gradients. The presented solutions provide excellent benchmark tests for the calculation of pressure changes in systems where large volumetric deformations are expected. Such systems include, but are not limited to, inflating magma chambers, metamorphic rocks with significant ΔV of reactions, phase transitions and other variants of geological compressible flows.

2. VOLUME BEHAVIOR OF MINERALS AT HIGH PRESSURE

Over the recent years, several internally consistent thermodynamic databases have been published with the aim to be used in mineral thermobarometry and phase equilibria applications (Berman, 1988; Chatterjee et al., 1998; Gottschalk, 1996; Helgeson et al., 1978; Holland & Powell, 1998, 2011). All minerals, within such databases, are treated as elastically isotropic solids, an approximation that we will also follow here. Nevertheless, it has been widely recognized that the volume behavior of minerals (EOS) is non-linear, thus implying that the thermal expansion and the bulk moduli of minerals should not be taken as constants apart from when small P-T ranges are considered. A review for the available EOS and their parameterizations is beyond the scope of this work, and the interested reader can find the relevant information in the cited literature (Anderson, 1995; Angel, 2000; Angel et al., 2017, 2018). In the remaining of this work, we will focus on isothermal mechanical solutions and we will investigate the effects of large compression/decompression in various host-inclusion pairs. Regarding the elastic problems, our approach is general, and it is not restricted to isothermal cases only (see section “NON-ISOTHERMAL ELASTIC CASES” for details).

We will first focus on the major non-linearity in the isothermal volume behavior of minerals, that is the pressure dependence of the bulk modulus. The consideration of a linear pressure dependence of the bulk modulus leads to the widely known Murnaghan EOS (Murnaghan, 1944). Murnaghan’s EOS has been widely used in Earth Science and it has been suggested that it yields accurate volume predictions of minerals for pressures below 20 GPa (Holland et al., 1996). The currently available calibrations of the Murnaghan EOS consider an extended range of minerals and they have been fitted with a focus on the internal consistency of the thermodynamic database (Holland & Powell, 1998). In order to increase the accuracy of the mineral P-V behavior with increasing pressure, we refitted the original volume data for some commonly studied minerals for pressures up to 20 GPa (table 1). The results show that the volumetric strain ($\epsilon_{V}$) of minerals for a large pressure range can be well described by a non-linear EOS whereas our calibration yields a relative volume error of less than 0.5% for the whole calibration range (fig. 2; see table 1 for details). The volumetric strain is calculated as the volume difference normalized to the initial volume, following the engineering strain notation (see Appendix A; eq A3).

Figure 2.Volumetric (engineering) strain as a function of hydrostatic pressure for commonly considered minerals.

Solid lines indicate fit using the Murnaghan EOS with data from table 1. Linearized (constant compressibility) EOS is shown with dashed line for comparison.

3. LOADING/UNLOADING OF HOST-INCLUSION SYSTEMS

As it was previously mentioned, the main reason for the development of pressure/stress differences in a host-inclusion system is the difference in the volumetric response of materials as a function of P-T changes. Another reason could also be the addition of material in a magma chamber beneath a volcano. In fact, this problem can also be reduced to the pressurized-inclusion problem (Dragoni & Magnanensi, 1989). However, in the magma-chamber case the effects of free-surface could be significant and may need to be included (e.g., Bonafede et al., 1986; McTigue, 1987; Mogi, 1958). This kind of behavior, commonly also known as the “pressure vessel”, is equally applicable across all geologically relevant scales. For example, it has previously been considered in order to explain the preservation of micrometer-scale coesite inclusions in garnet from UHP rocks (Chopin, 2003; Gillet et al., 1984; O’Brien & Ziemann, 2008; Perrillat et al., 2003). The preservation of the pressure/stress variations in pressure vessels from the geological record depends on many factors, with a major factor being the extent of mechanical relaxation that results from inelastic deformation (Dabrowski et al., 2015; Nye & Mott, 1953; Y. Zhang, 1998; Zhong, Moulas, et al., 2020; Zhukov & Korsakov, 2015). Such effects have been recently documented experimentally in mineral inclusions as well (Campomenosi et al., 2023). In the case where the physical conditions were such that irreversible deformation can be ignored, elastic rheology can describe both the volumetric and shear deformation in the host and the inclusion. In that case, the most essential part for the volumetric deformation of pure substances and reacting tight (non-porous) metamorphic rocks is the reversible elastic deformation. As a consequence, an accurate description for the large elastic volumetric deformation is necessary for minerals and tight rocks that can be described by path-independent EOS and phase-equilibria methods.

In order to state the host-inclusion problem more formally, we follow the explanation outlined in Rosenfeld and Chase (1961) and we briefly summarize it below. We begin by considering a host-inclusion mineral system at some hydrostatic conditions $P_{1}$ and $T_{1}$ where pressure and temperature is homogeneous throughout the host-inclusion system (fig. 3). By hydrostatic we mean that the stress tensor is isotropic and all the normal-stress components are equal. In this example, the host is considered to be much larger than the inclusion. Changing the pressure and temperature (to the new conditions $P_{2},T_{2}$) would impose a volume change in both phases. It is assumed that there is no difference between the temperature of the host and the inclusion as required by the relative fast thermal diffusion timescales at the mineral scale. We note that for a length scale of ~1 mm, and typical mineral thermal diffusivities of ~10^-6 m²/s, the characteristic thermal-diffusion timescale is ~1 second. Thus, due to the variability in the thermo-mechanical properties of minerals, the stress in host-inclusion systems does not have to be homogenous. This inhomogeneity is a consequence of stress balance and has also been observed using spectroscopic techniques (e.g., Howell et al., 2010; Murri et al., 2018). The mineral host generally experiences the pressure $P_{2}$ on the outer boundary and its basic state is assumed to have a homogeneous pressure distribution equal to $P_{2}$. This is generally a valid assumption in the case where the host is much larger than the inclusion. By virtue of the strain compatibility condition, and for linear-elastic rheology, the homogeneous pressure distribution is also true for the host even in the presence of a pressurized inclusion (see Appendix B for derivation). The basic state is defined as the state of the host if the inclusion is not there. In the presence of a mineral inclusion, the inclusion will not expand/contract freely but will also interact with the host (elastic interaction). In the case where the host and inclusion expand/contract by the same amount, there is no strain difference that develops between the two phases (both phases experience the same volumetric deformation). The particular set of conditions where there is no strain difference is described by the isomeke line in the P-T space (Adams et al., 1975; Angel et al., 2015; Rosenfeld & Chase, 1961). In the case of differential expansion/contraction, the difference in the volumetric strain of the two phases will result to an additional stress/pressure in the host-inclusion system (see Appendix C for details). The additional stress/pressure can be viewed as a perturbation of stress/pressure ($\Delta\sigma,\Delta P$) from the basic state of the host ($P_{2},T_{2}$). Under spherically-symmetric far-field loads, a spherical, homogeneous inclusion inside an isotropic homogeneous host will have a hydrostatic stress state and the normal stresses will be equal. Thus, the final pressure of the inclusion ($P_{3}$) can be estimated via equation (1) given below:

$$P_{3}^{i} = P_{2}^{h} + \Delta P^{i} \tag{1}$$

where the superscript $i$ indicates properties for the inclusion and $h$ for the host. This solution is an approximation that seems to be very accurate when spherical crystals are enclosed in relatively large hosts (Mazzucchelli et al., 2018; Zhong et al., 2021).

Figure 3.Sketch illustrating the development of volumetric strain and pressure difference in a host-inclusion system.

The thin white circle indicates the size of the inclusion for which no strain difference is developed. Residual elastic stresses develop in the case of a mismatch between host and inclusion volumetric strains (see text for more details).

4. MECHANICAL SOLUTIONS

4.1. Mechanical Solutions Assuming Linear Elasticity

There are several ways to obtain $\Delta P^{i}$ from equation (1) and each method has different assumptions. The simplest assumption is to consider that the volumetric deformation can be described by constant elastic moduli $a$, $K$ and $G$ which represent the thermal expansion, the bulk modulus and the shear modulus (rigidity) respectively. Moulas et al. (2020) reviewed the relevant literature that concerned the linear-elastic analytical solutions used in elastic geobarometry and concluded that the most appropriate solutions were the ones of Zhang (1998) and the one of Van der Molen and Van Roermund (1986). We note that this solution has its roots in the analytical solution of Lamé for a pressurized cylinder (Lamé & Clapeyron, 1831). Since the linear-elastic solution will be used as a reference, we show the solution below (Moulas et al., 2020; their eq 2, after Y. Zhang, 1998; taken at the linear-elastic limit where the host is infinite):

$$\scriptsize{ \begin{align} P_{fin}^{i} &= \biggl\{ \bigl( P_{ini}^{i} - P_{ini}^{h} + P_{fin}^{h} \bigr)\left\lbrack \frac{1}{K^{h}} + \frac{3}{4G^{h}} \right\rbrack \\ &\quad\quad + \left\lbrack P_{ini}^{i}\bigl( \frac{1}{K^{i}} - \frac{1}{K^{h}} \bigr) + \bigl( \bigl( \alpha^{i} - \alpha^{h} \bigr)\Delta T \bigr) \right\rbrack \biggr\} \\ &\quad /{\left\lbrack \frac{1}{K^{i}} + \frac{3}{4G^{h}} \right\rbrack} \end{align} } \tag{2}$$

$i$ and $h$ (superscripts) refer to the inclusion and the host respectively. The subscripts “$ini$” and “$fin$” refer to the initial and final conditions respectively. The thermal expansion of host/inclusion is $\alpha$ and the temperature difference between the final and the initial temperature is given by $\Delta T = T_{fin} - T_{ini}$. In our specific case $P_{ini}^{i} = P_{ini}^{h} = P_{1}$, $P_{fin}^{h} = P_{2}$ and $P_{fin}^{i} = P_{3}$. The linear elastic solutions can serve as a first-order estimate and can be accurate if the predicted strains are sufficiently “small”. From a more quantitative perspective, “small” strain increments result when the stress/pressure changes are considerably smaller than their respective elastic moduli. As an example of a small strain, we can consider an elastically stiff mineral host such as garnet. The pressure increase ($\delta P$) resulting from an increase of 1% in hydrostatic compressive (negative) volumetric strain (${\delta\epsilon}_{V}$) for a pure pyrope crystal ($K$~190 GPa) would be ~1.9 GPa ($\delta P = - K{\delta\epsilon}_{V}$).

4.2. Mechanical Solutions Assuming Non-linear Volumetric Behavior

There are many cases where the linear-elastic approximation may be inadequate. One case is the inherent non-linear EOS of minerals at large pressures (fig. 2). For petrology applications such as the quartz-in-garnet geobarometry, this nonlinearity can be approximated by the incremental application of equation (2). In this case, the P-T path of the host is discretized in small increments and the pressure of the inclusion is calculated using equation (2). During this procedure, the thermo-elastic moduli are updated according to the respective P-T conditions. This approach however is sensitive to the magnitude of the thermoelastic moduli and becomes less accurate near phase transitions, such as the α-β quartz lambda transition, where the effective elastic moduli are changing significantly and are practically discontinuous (Moulas et al., 2020). Furthermore, a second case where the linear approximation can be inadequate is the case of first-order phase transitions and melting that are characterized by large and discontinuous volume changes. A third case where the non-linear volume behavior may become important is the consideration of fluid and melt inclusions. Despite their negligible shear strength, fluids and melts are quite compressible and their volume behavior can be highly non-linear.

As it was previously mentioned, it is not the actual volumetric strain but rather the difference in the volumetric response of minerals which is responsible for the development of pressure variations between host and inclusions. For the case of a spherical and isotropic host-inclusion system, the inclusion will always experience a hydrostatic state of stress and, therefore, the only relevant deviatoric stresses are the ones of the host. Thus, the deviatoric stresses that develop as a response to a compression/decompression within the host will always be smaller in magnitude than the total amount of compression/decompression $\left| P_{2} - P_{1} \right|$. The previous considerations suggest that it is reasonable to consider a host inclusion system where the mineral volumes (which depend on the volumetric strain) are treated by non-linear, high-order EOS and the deviatoric stresses (which depend on the difference of the volumetric strains) are described using a linear-elastic approximation. This means that although the bulk modulus and the thermal expansion can be generally P-T dependent, the shear modulus (rigidity; $G$) of the host is considered constant. This allows a fast and straightforward method for the calculation of inclusion-pressure perturbation ($\Delta P$) which is given by the following formula (see Appendix C for derivation; Moulas et al., 2021):

$$\scriptsize{ \Delta P^{i} = 4G^{h}\left\lbrack 1 - \left( \frac{V_{fin}^{h}\left( P_{2},T_{2} \right)}{V_{ini}^{h}\left( P_{1},T_{1} \right)} \cdot \frac{V_{ini}^{i}\left( P_{1},T_{1} \right)}{V_{fin}^{i}\left( P_{3},T_{2} \right)} \right)^{\frac{1}{3}} \right\rbrack } \tag{3}$$

In the case where temperature is constant ($T_{1} = T_{2}$), and the volume of the host/inclusion is described by the Murnaghan EOS, the previous relation (eq 3) reduces to:

$$\scriptsize{ \Delta P^{i} = 4G^{h}\left\lbrack 1 - \left( \frac{\left( 1 + \left( P_{2} - P_{1} \right)\frac{K_{h}^{'}}{K_{h}} \right)^{- \frac{1}{K_{h}^{'}}}}{\left( 1 + \left( P_{3} - P_{1} \right)\frac{K_{i}^{'}}{K_{i}} \right)^{- \frac{1}{K_{i}^{'}}}} \right)^{\frac{1}{3}} \right\rbrack } \tag{4}$$

where $K_{i,h}$ is the bulk modulus of the phase $i,h$ at the initial P-T conditions ($P_{1},T_{1}$) and $K_{i,h}’$ is the pressure derivative of the bulk modulus (constant). The bulk modulus is given from:

$$K = K^{0} + K'(P - P^{0}) \tag{5}$$

where $K^{0}$ is the bulk modulus at the temperature of interest and at pressure $P^{0}$ (see table 1 for representative values at room P-T conditions).

A similar solution to equation (3) was given by Guiraud and Powell (2006) and it is shown below:

$$\scriptsize{ \Delta P^{i} = - \frac{4G^{h}}{3}\left\lbrack \frac{V_{fin}^{h}\left( P_{2},T_{2} \right)}{V_{ini}^{h}\left( P_{1},T_{1} \right)} - \frac{V_{fin}^{i}\left( P_{3},T_{2} \right)}{V_{ini}^{i}\left( P_{1},T_{1} \right)} \right\rbrack } \tag{6}$$

This solution appears as a limiting case in the earlier work of Zhang (1998, after his eq 19). Guiraud and Powell (2006) did not provide a detailed derivation for their equation and therefore it is not clear how they arrived at their final formula. By utilizing a large-strain approximation (Appendix C), we can demonstrate that equation (6) is a linearized version of our equation (3) (see Appendix D for details). Therefore, the accuracy of equation (6) will be limited when considering large P-T changes and/or highly compressible phases. The reason for this discrepancy is related to how the strain difference is calculated. In the case of Guiraud and Powell (2006), their formulation (eq 6) provides a pressure difference directly proportional to the strain difference. This form is accurate only for very small volumetric-strain mismatch between the host and the inclusion and it is expected to become less accurate with the increasing difference of volumetric strains. More recently, Zhong, Dabrowski, et al. (2020) utilized the logarithmic strain in order to describe the volumetric-strain mismatch between the host and the inclusion. Their results lead to a more accurate expression for eq 6 (see Appendix D for details).

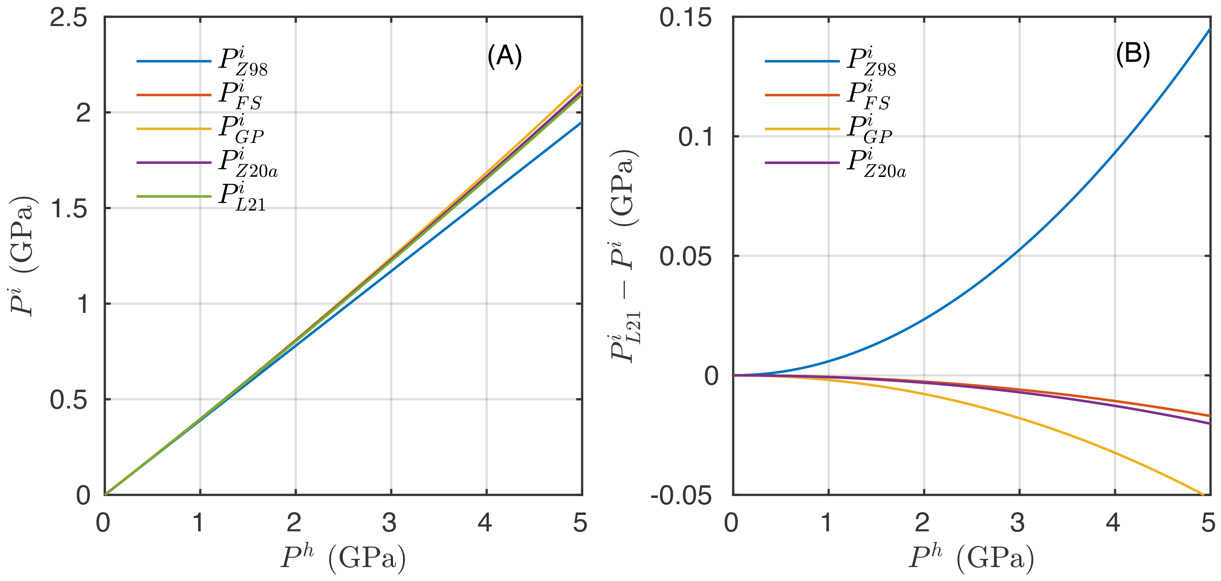
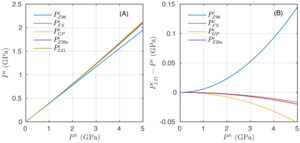
In order to compare the different approximations, we performed a convergence analysis using a numerical solution that takes into account the non-linearities of the EOS of minerals. The numerical solution uses the implementation of Zhang’s (1998) linear-elastic solution (assuming infinite host, as in eq 2) in a finite number of discretized steps following the procedure that was described in Moulas et al. (2020). At each increment, the elastic constants are updated with the respective values ($G^{h}$ is considered constant). With increasing resolution, the numerical solution converges towards the solution given by Zhong, Dabrowski, et al. (2020), (fig. 4). Our solution given by equation (3) is very close to the solution of Zhong, Dabrowski, et al. (2020) with the difference being less than 1 MPa (fig. 4). Compared to our approach (eq 3), the approach of Zhong, Dabrowski, et al. (2020) utilizes the logarithmic strain as a strain measure (see Appendix D for details). The solution of Guiraud and Powell (2006) seems to have a systematic difference from all the other non-linear solutions and we attribute that to an error that is introduced by the infinitesimal-strain approximation as suggested also by Zhong, Dabrowski, et al. (2020). Although the error is initially small when small pressure ranges are considered (fig. 4a), the error progressively increases when the amount of compression/decompression is larger as expected (fig. 4b).

Figure 4.Convergence results for the calculation of the final residual pressure ($P_{fin}^{i}$) of an $a$-quartz inclusion in almandine garnet (isothermal case).

The results are given as a function of the path-resolution of the numerical calculation (path increments). Both phases were assumed to be at the same initial pressure. In both cases (a,b) we have assumed the isothermal decompression of the host-inclusion systems (at room $T$). The EOS parameters are as in table 1. The solution of “this work” is after eq (4). The value derived using a purely linear-elastic solution ($P_{lin}$) is shown for comparison. (A) Host decompression is 1 GPa. (B) Host decompression is 3GPa.

4.3. Fully Non-linear, Finite Strain Elastic Solutions

In the previous section we considered the case of a host-inclusion system where the volumetric strain of host and inclusion are described by non-linear EOS. Still, the non-hydrostatic (deviatoric) stress components, of the host, have been approximated by linear-elasticity theory. To see the effect of non-linear elasticity, we have to consider the fully non-linear behavior of the host as well. Yet, the extension to non-linear elasticity cannot be performed by ad-hoc incorporations of the P-T dependence of the elastic moduli (see also Moulas et al., 2020). This is because, non-linear elasticity implementations have to be thermodynamically consistent and have to guarantee the path-independence of the results. For these criteria to be satisfied, the stresses should be obtained via a thermodynamic potential such as the one shown below (for example, Lurie, 1990; Ogden, 1984):

$$S_{jk} = \left( \frac{\partial W}{\partial E_{jk}} \right) \tag{7}$$

where $W$ is a strain-energy density function (in Pa), $S_{jk}$ are components of the second Piola-Kirchhoff stress tensor S (in Pa), and $E_{jk}$ are components of the Green strain tensor $\mathbf{E}$ (dimensionless). These tensors are defined as follows:

$$\mathbf{E} = \frac{1}{2}\left( \mathbb{C -}\mathbf{I} \right) = \frac{1}{2}\left( \mathbf{F}^{T}\mathbf{\cdot F} - \mathbf{I} \right) \tag{8a}$$

$$\mathbf{S} = J\mathbf{F}^{- 1}{\cdot \mathbf{\sigma} \cdot \mathbf{F}}^{- T} \tag{8b}$$

where $\mathbf{F}$ is the deformation gradient, $J = \det\mathbf{F}$, and $\mathbb{C}$ is the Green (Lagrangian) deformation tensor:

$$\mathbb{C} = \mathbf{F}^{T}\mathbf{\cdot F}, \tag{9}$$

$J$ is the Jacobian of the deformation gradient tensor and it is also equal to the volume ratio of the final to the initial state ($V^{fin}/V^{ini}$). In particular, the dependence between the tensors S and E can be linear:

$${S_{jk} = C}_{jklm}E_{lm}\tag{10}$$

where $C_{jklm}$ are components of the elastic stiffness tensor.

For an isotropic material, the strain energy density function at constant temperature can be given as a function of the invariants of the Green (Lagrangian) deformation tensor $\mathbb{C}$ (Lurie, 1990; Ogden, 1984). Levin et al. (2021) recently derived the following form of strain-energy density function

$$\small{ \begin{align} W\left( {\widehat{i}}_{1},{\widehat{i}}_{3} \right) &= 2G({\widehat{i}}_{1} - 3) \\ &\quad + \frac{K^{0}}{K'\left( K^{'} - 1 \right)}\left\lbrack {\widehat{i}}_{3}^{- \left( K^{'} - 1 \right)} + \left( K^{'} - 1 \right){\widehat{i}}_{3} \right\rbrack \end{align} } \tag{11}$$

where ${\widehat{i}}_{1}$ and ${\widehat{i}}_{3}$ are invariant forms defined as shown below:

$$\begin{align} \hat{\imath}_1&=\left(\lambda_1+\lambda_2+\lambda_3\right)-3 \hat{\imath}_3^{\frac{1}{3}} \\ \hat{\imath}_3&=\lambda_1 \lambda_2 \lambda_3=J \end{align} \tag{12}$$

and $\lambda_{j}$ are the principal stretches in the spherical coordinate system. For the spherically symmetric host-inclusion problem, only the normal stresses in the principal directions are non-zero. Thus, the true (Cauchy) stress components ($\sigma_{j}$) for the spherically symmetric coordinate system are given by:

$$\sigma_{j} = \frac{\lambda_{j}}{J}\left( \frac{\partial W}{\partial\lambda_{j}} \right) \tag{13}$$

The strain-energy density function of equation (11) is a specific case for a generalized Varga material (Horgan, 2001) and it reduces to the isothermal Murnaghan EOS (Anderson, 1995; Murnaghan, 1944) for pure-hydrostatic compression, i.e.:

$$P = \frac{K^{0}}{K'}\left\lbrack \left( \frac{V_{fin}}{V_{ini}} \right)^{- K^{'}} - 1 \right\rbrack \tag{14}$$

where $K^{0}$ and $V^{ini}$ are evaluated at zero strain and zero pressure. At the limit of small strains, the shear modulus (rigidity) of the material reduces to the constant $G$ in (eq 11). Thus, $G$ in equation (11) should be viewed as a small-strain limiting value whereas the actual effective shear modulus can be obtained by differentiation of equation (11). In fact, the dependence of the strain-energy density on strain accounts for the fact that the effective elastic moduli are pressure dependent (physical non-linearity).

Levin et al. (2021) presented analytical solutions for the compression of the hollow-sphere problem by considering hosts that are characterized by the potential of equation (11). Figure 5 shows the normal stress components of a pressurized quartz inclusion in an almandine host. The initial stress of the host and the inclusion is assumed to be homogeneous and equal to room pressure conditions. At the final state, the host experiences a compressive normal stress of 5 GPa at its outer boundary (fig. 5). The inclusion experiences homogeneous hydrostatic stress conditions and its pressure can be evaluated by Murnaghan’s EOS (eq 14). Figure 5 shows that for a host compression of 5 GPa, the inclusion experiences a pressure of ca. 2 GPa. The difference between the two solutions, linear and non-linear, is very small in this case (fig. 5). The mean stress in the host is nearly homogeneous and its variation is of the order of 2 MPa (fig. 5). We note however, that in the linear-elastic solution the mean stress of the host must remain constant (Appendix C). Furthermore, the fact that the mean stress of the host is nearly homogeneous (or constant in the linear-elastic case) does not mean that the mean stress in the host is also equal to the normal stress that is applied at the outer boundary. This is a good approximation when the host is much larger than the inclusion, but it is not generally the case.

Figure 5.Normal stress components for the case of a stressed quartz inclusion within an almandine host.

The distance is normalized to the initial radius of the inclusion. The outer radius of the host is 10 times larger than the radius of the inclusion (only the inner part of the host is shown). The solid lines are evaluated using the solution of Levin et al. (2021). The doted lines are evaluated using the linear elastic solution (for example, Bower, 2009; Y. Zhang, 1998). Note that since stresses are positive in extension and pressure is positive in compression, the stresses are plotted with opposite sign.

The previous example shows that, for the isothermal loading/unloading, even the linear elastic solution can be a good approximation in predicting the pressure of the inclusion. To demonstrate this point, we plot the various inclusion-pressure predictions ($P^{i}$) as a function of the loading of the host (fig. 6). Figure 6a shows that the non-linear solutions (Guiraud & Powell, 2006; Levin et al., 2021; Zhong, Dabrowski, et al., 2020; and eq 3 from this work) are very close to each other and predict larger pressure differences compared to the linear-elastic solution (fig. 6a). However, if one considers the difference from the fully non-linear solution of Levin et al. (2021), it can be shown that equation (3) is the closest, albeit simple, approximation (fig. 6b). The difference between the fully non-linear solution and the solution of Zhong, Dabrowski, et al. (2020) is also very small, however it is larger than the difference of eq 3 (fig. 6b).

Figure 6.

A) Pressure evolution for the inclusion as a function of the outer pressure of the host. The different lines correspond to different elastic solutions, Z98: linear-elastic limit of Zhang (1998), FS: Finite volumetric strain (eq 3), GP: Guiraud and Powell (2006), Z20a: Zhong, Dabrowski et al. (2020), L21: Levin et al. (2021). B) Difference of the various solutions from the solution of Levin et al. (2021) as a function of the outer pressure of the host.

5. NON-ISOTHERMAL ELASTIC CASES

Despite the consideration of a large compression/decompression ranges in some of the previous solutions, their practical usage in non-isothermal scenarios requires additional models. Although the volumetric behavior of minerals is well constrained with respect to temperature, most of the available shear moduli are constant and do not include a temperature dependence. As it was already highlighted in Moulas et al. (2020), empirical fits that describe the $T$ and $P$ dependence of the shear moduli will probably lead to violations of thermodynamic relations that would render the elastic solutions path dependent. This problem can be mitigated when the stress can be obtained via a thermodynamic potential as shown in equation (7). Up to date, there are very few potentials that can be used for the large-strain of minerals (Clayton, 2013). In addition, incorporating the effects of temperature would require the modification of elastic potential in equation (11). These problems can be circumvented by exploiting the path-independence of the solution of the host-inclusion problem (Moulas et al., 2020). That is, we can make use of the isomeke lines in order to convert the general host-inclusion problem into an isothermal problem (Angel et al., 2014, 2015). The advantage of the isomeke line is that, along this line, the relative volume change of the host matches exactly the relative volume change of the inclusion. Therefore, any elastic calculation can be split into two steps. The first step is to consider the calculation of the intersection of the isomeke line at the necessary temperature (also known as $P_{foot}$; Angel et al., 2014). Then, the host’s compression/decompression calculation (e.g., from $P_{foot}$ to $P_{fin}^{h}$) can be completed by one of the isothermal elastic calculations that we considered previously (for example, linear, non-linear EOS, or fully non-linear). In most elastic-thermobarometry applications, the temperature of interest, where $P_{foot}$ is calculated, is the room temperature. The separation of the host-inclusion loading/unloading path into these two parts (isomeke and isothermal) allows the consideration of complex hyperelastic materials where only the isothermal strain-energy function is known, such as in our case.

Using the isomeke curve as a tool for the calculation requires the knowledge of the shear elastic moduli at constant temperature. When an elastic potential is not available, then, shear moduli can be taken from experimental measurements assuming a low strain assumption. This is advantageous since most of the available measurements in minerals concern measurements at room temperature (e.g., Milani et al., 2015; J. Wang et al., 2015; Z. Wang & Ji, 2001; L. Zhang et al., 1999). Using constant values may not cause large discrepancies as shown in figure 6. However, some of the available moduli correspond to the adiabatic elastic moduli (see also Babuška et al., 1978). In that case, the choice of the appropriate moduli depends on the characteristic frequency of the process that is investigated. For mechanical applications, that consider isothermal mechanical equilibrium between the host and the inclusion, the isothermal moduli should be preferred. The adiabatic and isothermal moduli are related by (Fung, 1965, p. 389):

$$\begin{aligned} \left( C_{jklm} \right)_{T} &= \left( C_{jklm} \right)_{S} \\ &\quad - \frac{T_{0}}{\rho C_{V}}\beta_{jk}\beta_{lm} \end{aligned} \tag{15}$$

where $C_{jklm}$ is the (4^th rank) elastic stiffness tensor (in Pa) and the subscripts $S$ and $T$ indicate adiabatic and isothermal conditions respectively. $T_{0}$ indicates the temperature of reference (in K), $\rho$ is the density (in kg/m³), $C_{V}$ is the mass-specific heat capacity at constant volume (in J∙K^-1∙kg^-1) and $\beta_{jk}$ are the thermal moduli (in Pa∙K^-1). The thermal moduli are given by (Fung, 1965, p. 387):

$$\beta_{jk} = - \left( \frac{\partial\sigma_{jk}}{\partial T} \right) \tag{16}$$

In practice, the difference of the two moduli (adiabatic and isothermal) can be negligible for petrological applications of host-inclusion systems. For example, the difference in the adiabatic and isothermal bulk moduli of almandine at room conditions is around 3% (Babuška et al., 1978; Milani et al., 2015). However, the difference may be more than apparent when elastic (seismic) velocities are calculated (Connolly & Kerrick, 2002).

For the cases where the shear moduli can be considered constant, the isothermal part of the calculation simplifies greatly. In fact, when elastic thermo-barometry applications are considered, the solutions provided by equations (3) and (4) can provide the residual inclusion pressure in a single step without the consideration of cooling/decompression along the isomeke curve. This result has been demonstrated also by incremental numerical calculations (Moulas et al., 2020). The reason why this is the case is because the strain energy function that results from an isotropic compressible material and also has a constant shear modulus (rigidity) satisfies equations (7) and (10). A necessary requirement for the previous statement is that the volume should be given by an EOS and, thus, any volume changes should be path independent.

6. ELASTO-PLASTIC MODEL

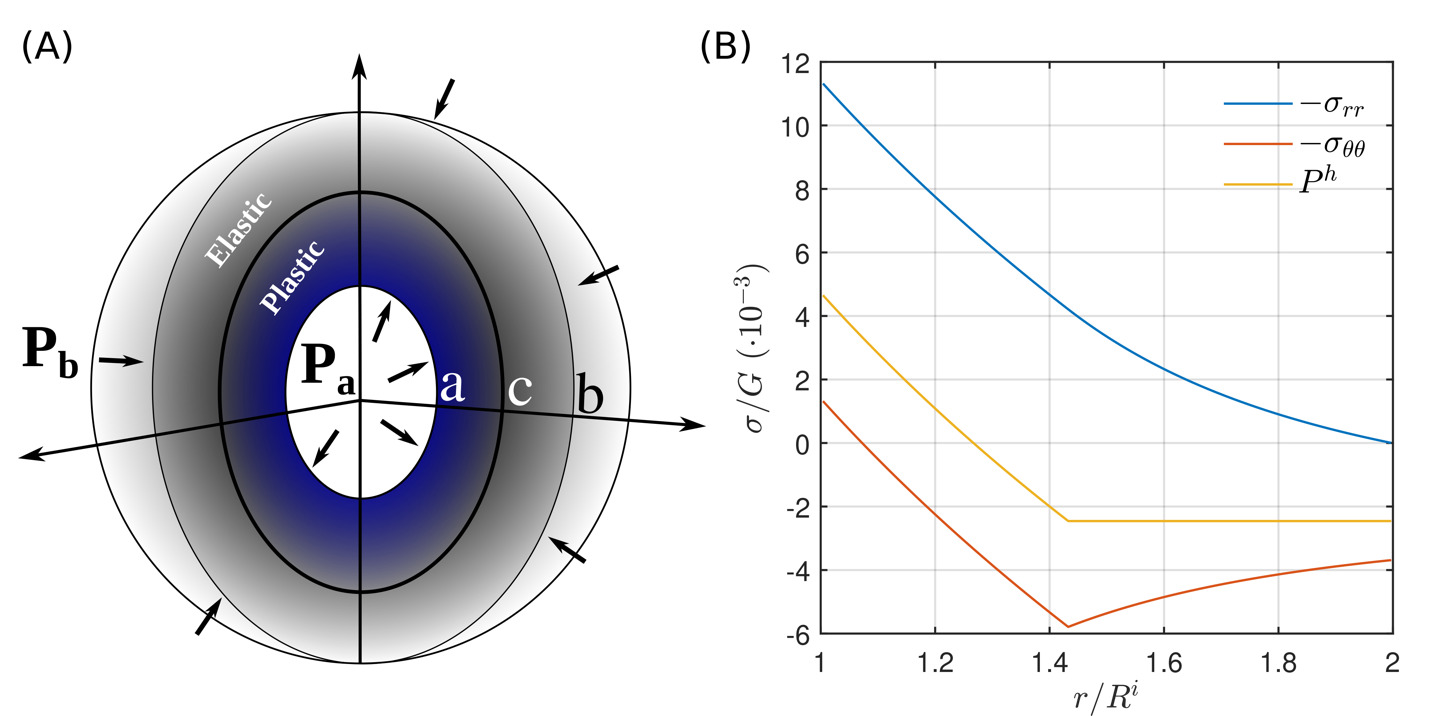
As mentioned also in the previous section, the linear elastic solution is more appropriate for relatively small strains. Nevertheless, due to the large values of the elastic moduli, the stresses that develop during loading or decompression of mineral host-inclusion systems are large and can reach the yield stress of the host crystal. In this case, it is quite probable that an internal, highly-stressed zone develops adjacent to the inclusion where the differential stress is entirely determined by the ability of the host to sustain shear deformation (see for example, fig. 7a).

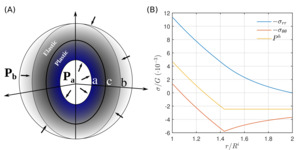
As an example, we show such a case where the host is loaded as a response of the increasing internal pressure of the inclusion (fig. 7b). If we consider that the internal pressure is approximately 1% of the shear modulus of the host, for the case of a mineral like garnet ($G \approx 90$ GPa), this would mean that the internal pressure is in the order of ~0.9 GPa. If now the host mineral can sustain differential stress in the order of ~1% of the shear modulus, then a plastic zone will develop between the inclusion-host interface (point $a$ in fig. 7) and a point within the host (point $c$ in fig. 7). For a constant yield stress, like in the case of a von Mises plastic model, this problem is considered classic in the engineering literature and it admits exact analytical solutions (e.g., Bower, 2009; Hill et al., 1947; Kachanov, 1971). Figure 7b shows the distribution of the stress components and pressure such a model. It becomes apparent that the development of a plastic zone within the host leads to the development of mean stress (pressure) gradients (fig. 7b). In fact, since the mean stress is the average of the normal-stress components ($P = - (\sigma_{rr} + 2\sigma_{\theta\theta})/3$), the weaker the material becomes, the more pronounced the pressure gradients will be within the plastic zone.

Figure 7.

A) Sketch illustrating the elasto-plastic spherical host. A spherical host is pressurized from within. The pressure at the inner surface of the host is $P_{a} = \left. \ - \sigma_{r} \right|_{r = a}$, and the pressure at the outer surface of the host is $P_{b}\left. \ = - \sigma_{r} \right|_{r = b}$. The region $r \in \lbrack a,c\rbrack$ is characterized by plastic deformation and the outer region, $r \in \lbrack c,b\rbrack$ , is considered to be elastic. B) Stress distribution within an elastoplastic host. The elastic part of the deformation is described by linear elasticity where the bulk modulus is two times larger than the shear modulus. The plastic deformation is described by von Mises plasticity where yield stress is constant and equal to 1% of the shear modulus. All stress and pressure components have been normalized to the shear modulus of the host (see text for more details).

The limitation imposed by plastic deformation on the development of differential stress has a direct consequence on the pressure of the inclusion in a host-inclusion system. This is because the differential stress of the host and the pressure difference from the inclusion are related (see also Appendix C). For a host that is much larger than the inclusion, the pressure difference between host and inclusion will be equal to the deviatoric radial stress ($\tau_{rr})$ that develops at the host-inclusion interface ($r = \alpha^{+}$), in particular:

$$P^{i} - P^{h} = - P^{h} - \left. \ \tau_{rr} \right|_{r = a^{+}} \tag{17}$$

Thus, if the magnitude of $\tau_{rr}$ is limited during plastic deformation, so will be the magnitude $P^{i}$. Figure 8 shows the development of a residual pressure difference as a function of the isothermal unloading of the host to zero pressure. Note that although the elastic effects become increasingly important at very large unloading values, plasticity has a dramatic effect in the preservation of the residual inclusion pressure.

Figure 8.Residual inclusion pressure difference as a function of the isothermal decompression of the host.

The dashed line is a linear elastic solution and is given for reference. Solid lines have been calculated using the Murnaghan EOS for both the host and the inclusion ($K’ = 4$ for both phases). The host is considered to be much larger than the inclusion. Both the residual and the unloading pressures have been normalized to the reference bulk modulus of the inclusion ($K_{0}^{i})$. The reference bulk modulus and the shear modulus of the inclusion are given by $K_{0}^{h} = 5K_{0}^{i}$ and $G^{h} = 3K_{0}^{i}$ respectively. For the elastoplastic case, a von Mises plasticity model has been assumed. The von Mises (differential) stress $\sigma_{Y}$ is taken to be 5% of the value of $G^{h}$.

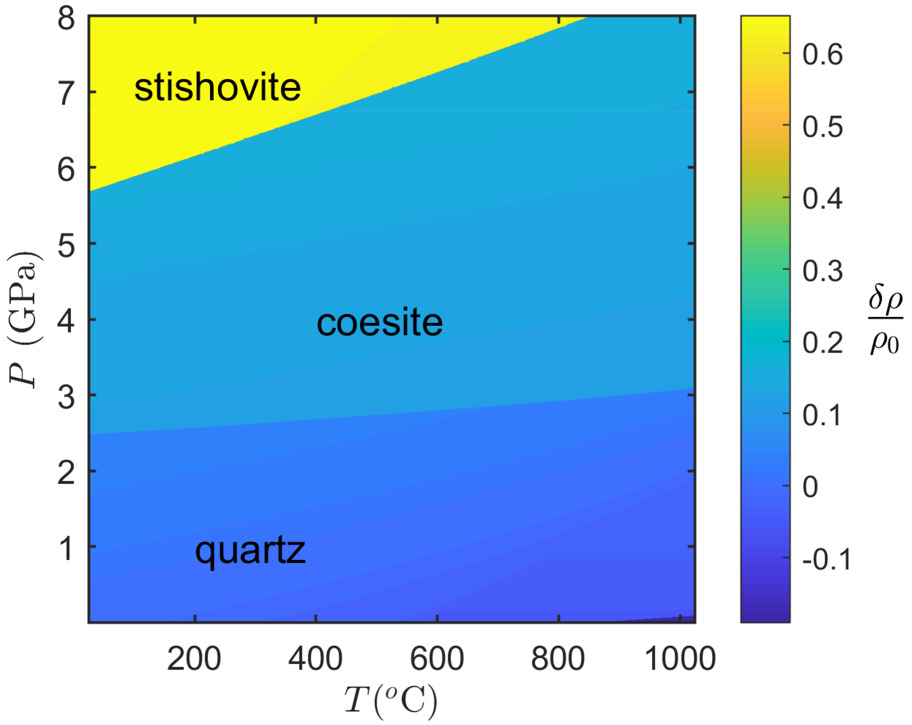
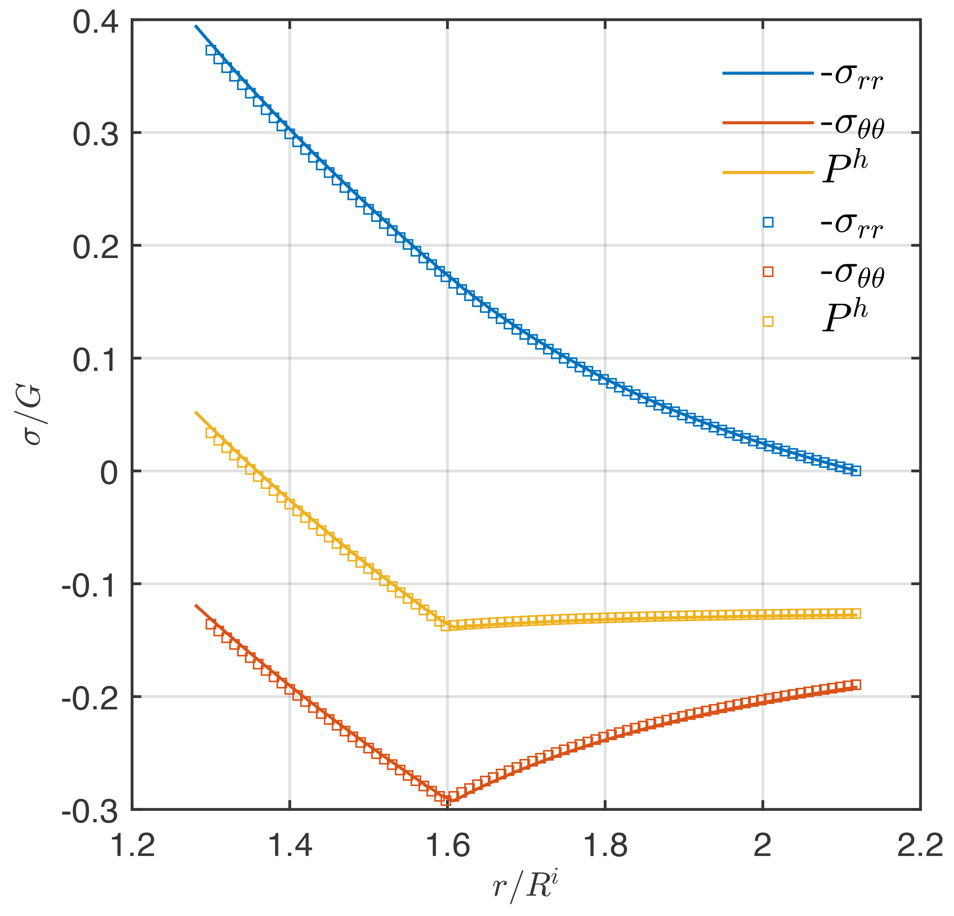
Elasto-plastic models like the previous one, are adequate for as long the stresses and the associated strains are relatively small. By small we mean that there is no significant difference between the deformed and the undeformed configuration. Rocks have in general more complex elastic and plastic rheologies. This becomes particularly important when the mineral/rock inclusions experience phase transitions and mineral reactions in general. Phase transitions and mineral reactions can typically have volumetric strains of the order of 10 to 20% or larger (fig. 9). In addition, a particular feature of rocks is that they exhibit pressure-dependent yield stress and they can have plastic volumetric deformation. To account for all these complexities, more elaborate models are needed that can be used as benchmarks in petrology and geodynamics studies. Figure 10 shows an example of a hyperelastic, plastic material that has experienced significant strain and has a pressure-sensitive, plastic deformation (Drucker-Prager model). This model is geometrically non-linear (large-finite strain) and also intrinsically non-linear with respect to its elastic and plastic behavior. The fact that the strain is significant can be demonstrated from the fact that the initial (undeformed) host is chosen to have the same size as in the case of the simpler model shown in figure 7b. However, it is clear that the large strain at the inner boundary of the host has led to observable differences between the deformed and the undeformed configurations (compare fig. 7b with fig. 10). For example, the inner boundary of the host is at $r/R \approx 1.3$ in figure 10 instead of $r/R \approx 1$ that is shown in figure 7b. This difference is significant when compared to small-strain elasto-plastic models. The details of the model are given in appendices E (for the numerical solution) and F (for the analytical solution). The results show that the proposed method is very accurate as it can be verified by the match of the analytical and the numerical solutions (fig. 10). The further development of this approach can be related with the modeling of physical/chemical processes in metamorphic rocks on the base of the theory of repeatedly superimposed finite strains (Levin, 1998; Levin, Levitas, et al., 2013).

Figure 9.Relative density changes of SiO₂ polymorphs with respect to the density of α-quartz at room conditions. This diagram was calculated using Perple_X (Connolly, 2009) and the thermodynamic database of minerals from Holland and Powell (2011).

Figure 10.Stress distribution for a hyperelastic-plastic host.

The parameter $K_{0}$ of the bulk modulus is 2 times larger than the parameter $G$ of the elastic strain energy function (eq 11), and the pressure derivative of the bulk modulus, $K’$, is equal to 4. The plastic deformation is described by a pressure dependent Drucker-Prager condition where the cohesion is equal to 25% of the shear modulus, the internal friction angle is 45° and the dilatancy angle is 30°. Solid lines indicate the results obtained from the numerical solution (Appendix E) and square symbols indicate the results obtained from the analytical solution (Appendix F).

7. DISCUSSION

The preservation of mineral inclusions which formed at high-grade metamorphic conditions have been used for many years in order to infer the physical/chemical conditions of metamorphic rock crystallization (see review of Ferrero & Angel, 2018). Mineral inclusions can provide both mineralogical and compositional data that can be of value for the petrogenetic interpretation of metamorphic rocks (e.g., Chopin & Sobolev, 1995; Spear & Selverstone, 1983). Due to the increasingly developed spectroscopic and diffraction techniques, the mechanical effects of mineral host-inclusion systems have been commonly used as independent means for the determination of pressure (sometimes also temperature) in metamorphic phase equilibria interpretations (Alvaro et al., 2020; Castro & Spear, 2017; Moulas et al., 2020; Szczepański et al., 2022; Zhong et al., 2019). So far, most of the solutions employed in the calculation of residual inclusion pressure assume spherically symmetric systems and materials which are elastically isotropic (Guiraud & Powell, 2006; Van der Molen & Van Roermund, 1986; Y. Zhang, 1998). In addition, numerical calculations that consider elastically stiff, isotropic mineral hosts and anisotropic mineral inclusions (such as quartz in garnet) have suggested that the effects of anisotropy in this case are minor (Mazzucchelli et al., 2019). Thus, apart from their value for code benchmarking, spherically symmetric and isotropic mineral host-inclusion systems are very useful for elastic geobarometry (or thermobarometry) applications.

An additional advantage of having spherically symmetric and isotropic solutions is that they allow the incorporation of internally consistent thermodynamic data for minerals. This is because all the currently available thermodynamic databases assume isotropic properties (Berman, 1988; Chatterjee et al., 1998; Gottschalk, 1996; Helgeson et al., 1978; Holland & Powell, 1998, 2011). The usage of internally consistent thermodynamic datasets can provide better constrains regarding the P-T dependence of the thermo-elastic moduli (bulk modulus and thermal expansion) for a large range of pressures and temperatures. However, treating host-inclusion systems that can support large strains would justify the usage of non-linear elastic solutions. A very popular solution is the one of Guiraud and Powell (2006) which considers the non-linear volume behavior as a function of P-T. In principle, this solution can be justified for problems that consider large volumetric strains. However, we have shown that the volume strain by Guiraud and Powell (2006) is a truncated form that applies only at the limit of small strains (see Appendix D for details). This causes a systematic error with increasing loading/unloading of the host inclusion system. To avoid this error, we proposed a new form (eq 3) that accounts for the effects of finite volumetric strain. The solution suggested by Zhong, Dabrowski, et al. (2020) yields also very similar results. Equation (3) considers that the shear stress, that results from the volumetric-strain mismatch between host and inclusion, is so small that it can be approximated by linear elasticity (constant shear modulus). This can be justified because the deviatoric stresses do not depend on the total strains that develop in a host-inclusion system, but they rather depend on the much smaller volumetric-strain mismatch among the two phases. For a more accurate treatment of the host inclusion problem a recently available solution developed for hyperelastic materials is utilized in this work (Levin et al., 2021). This solution reduces to the Murnaghan EOS for volumetric strains but is fully non-linear (geometrical and physical non-linearity) and can handle larger strains. In this approach, the elastic properties depend on a potential function for which it has been demonstrated that analytical solutions exist (Carroll, 1988). Despite the higher accuracy predicted by the solution of Levin et al. (2021), the actual differences from equation (3) are very small for practical purposes (fig. 6). Theoretically, such accuracy would be justifiable for elastic barometry applications and especially for hosts that experience large decompression ranges. Both approaches (eq 3 and the solution by Levin et al., 2021) can also be used for non-isothermal, elastic problems in combination to the isomeke line concept (Angel et al., 2014, 2015).

The non-linear solutions that are presented in this work become more important when one considers the cases of phase transitions and mineral reactions in general. That is because phase changes can lead to significant volumetric strains that may not be accommodated by small-strain elastic effects. For the particular case of SiO₂ polymorphs, these volumetric strains can reach the order of 60% but can be typically in the range of ~20% like in the case of quartz coesite-transition (fig. 9). Such large inclusion strains will impose a large amount of strain on the host as well. If this strain cannot be accommodated by the mineral hosts, then it is more likely that the transition will not be complete (Gillet et al., 1984). In the latter case, the host-inclusion system is mechanically buffered.

With increasing volumetric strain, stresses may build up in the surrounding rocks resulting to the development of plastic strains. In order to consider the plastic deformation of pressurized hosts (pressure-vessels) we have revisited the classical, elasto-plastic, hollow sphere problem (Hill et al., 1947). This classic problem is relevant for various scales in geosciences (Gerbault et al., 2012; Tajčmanová et al., 2014). What is clear from such models is that the pressure vessel effect does not require complete confinement since any value of stress can be imposed as an outer boundary condition (for example, figs. 7 and 10). This is of particular importance for regions within the Earth that experience large volumetric strains. In the case where stresses develop faster when compared to other relaxation phenomena (such as viscous creep), the plastic yield stress will be reached. In these cases, plasticity will limit the differential stress near the inflating/compacting region and a pressure gradient will develop in the host as a response to stress balance (figs. 7 and 10). Thus, assertions, such as the one suggested by Etheridge et al. (2021), that the pressure vessel model is not appropriate in geology since it requires complete confinement, have overlooked the fact that the boundary conditions used in the models provide a realistic representation of the conditions associated with “confinement”. Therefore, such statements are not mechanically justified.

The advantage of using analytical solutions or non-linear approximations, is that they can be used as a benchmark for numerical solution, which is especially important for determining the conditions required for numerical convergence (see for example, figs. 4, 6 and fig. 10). This is of particular use in applications that go beyond mineral elastic thermobarometry. For example, a reacting rock that experiences fast volume changes or an inflating magma chamber beneath a volcano can deform in very short timescales that would justify an elastic rheology (Luisier et al., 2019; McTigue, 1987; Mogi, 1958; Spang et al., 2021). The fact that magma and multiphase rocks are composed of many reacting phases can lead to effective elasticity parameters that cannot be described by simple mechanical models. Given the large values of the effective elastic moduli of geomaterials, the accurate description of volumetric deformation may lead to an increase of accuracy for stress calculations in the range of kbar (~100 MPa) level, which is already within the range of flow stress values that are typically predicted in geodynamic or volcano simulations (Bessat et al., 2020; Gerbault et al., 2012; Jaquet & Schmalholz, 2018). Thus, non-linear models of host-inclusion systems will also be useful when testing compressible geodynamic codes.

8. CONCLUSIONS

We have revisited the classic Lamé problem for its applications in petrology and geodynamics and we have tested various formulations that range from simple linear elastic rheologies to fully non-linear elastoplastic rheologies at large finite strains. In particular, we have focused on two approaches that consider finite-strain effects. In the first approach, only the volumetric part of the finite strain is considered (eq 3). The resulting analytical solution is in excellent agreement to converged numerical models (fig. 4). In the second approach, we considered a recently published model for hyperelastic materials that can be of use in petrological applications that require large strains (Levin et al., 2021). Although rarely used in geology, hyperelastic models offer a thermodynamically consistent framework for modeling non-linear elastic deformation. This is desirable in order to keep the elastic solutions path-independent, and therefore suitable for geo-thermobarometry purposes. Our results show that for common elastic thermobarometry applications, and without considering volume changes due to phase transitions or reactions, the geometrical non-linearity is not so crucial, and can be neglected. The simple non-linear model (eq 3) offers very accurate results while can be easily implemented for any non-linear volumetric EOS. Very similar results can be obtained by using the solution of (Zhong, Dabrowski, et al., 2020). Since our new solution can be used to calculate the exact volumetric deformation of spherical inclusions even for very large volumetric strains, our results can be used to benchmark numerical codes which aim to quantify the volumetric effects of mineral reactions and phase transitions in geodynamic applications. Finally, we have presented non-linear elasto-plastic solutions of the Lamé problem. Our results indicate that the effects of plasticity may become important for the cases of large-volumetric strains. The development of plastic strains leads to significant pressure gradients even in the simplest elasto-plastic models. Therefore, such solutions can offer an accurate way to check the pressure/stress formulation in compressible geodynamic codes that account for the pressure-dependent plastic yield.

ACKNOWLEDGMENTS

E.M. would like to acknowledge the Johannes Gutenberg University of Mainz for financial support. Y.P., K.Z., A.V. and V.L. were financially supported by Russian Science Foundation (project No. 19-77-10062) in the part related to the geomechanical problem statement and its analysis, and by Ministry of Education and Science of Russian Federation (grant №075-15-2022-1106) in the part related to the development of analytical and numerical algorithms for problem solving. Mattia Mazzucchelli is acknowledged for constructive criticism of an earlier version of this draft. Xin Zhong, Marcin Dabrowski, and an anonymous reviewer are acknowledged for constructive criticism that allowed us to improve the manuscript. Lucie Tajčmanová and Mark Brandon are acknowledged for the editorial handling and for constructive comments.

AUTHOR CONTRIBUTIONS

All authors contributed to the development of the ideas and writing of the manuscript. E.M., Y.P., K.Z. & V.L. derived the simplified analytical solution (e.g., eqs 3,4). V.L. made a key contribution to the mechanical and mathematical problem statement under finite strains with the account for finite preliminary strain leading to finite additional strain (Levin, 1998; Levin, Levitas, et al., 2013). V.L., K.Z. & A.V. developed algorithms of numerical and analytical solutions under finite strains (Appendices E and F). K.Z. and V.L. derived and calculated the analytical solution in Appendix F (based on Levin et al., 2021). A.V. and V.L. developed the software and calculated the numerical solution of Appendix E using spectral element method (Konovalov et al., 2017). All the other models were calculated by E.M.

DATA AVAILIBILITY

All the sources of the data used are explicitly mentioned in the text.

Editor: Mark Brandon, Associate Editor: Lucie Tajcmanova

APPENDICES

APPENDIX A

The Relations Between Linear and Volumetric Strain for the Host-Inclusion Problem

In this appendix we provide the derivation for the calculation of the strain that develops in the host at the host-inclusion interface. Both the host and the inclusion are considered to be isotropic. The volume (in m³) of a phase $m$ (indicated by superscript) at some arbitrary pressure and temperature (P-T) conditions can be obtained by:

$$\frac{M^{m}}{W^{m}}V^{m}(P,T) \tag{A1}$$

where $M$ is the mass of the phase (in kg), $W$ is its molecular weight (in kg/mol) and $V$ is the molar volume of the phase (in m³/mol). With changing P-T conditions, the volume of each phase is changing according to its Equation Of State (EOS). The ratio of (absolute) volumes between some final $\left( P_{2},T_{2} \right)$ and initial $\left( P_{1},T_{1} \right)$ conditions is thus given by:

$$R_{vol}^{m} = \frac{V_{fin}^{m}\left( P_{2},T_{2} \right)}{V_{ini}^{m}\left( P_{1},T_{1} \right)} \tag{A2}$$

where the subrscripts “fin” and “ini” indicate final and initial conditions respectively. Note that the absolute mass and the molar weight does not appear in the previous formula since they are constants and can be eliminated. The previous ratio is also related to the volumetric (engineering) strain ($\epsilon_{V}$) as follows:

$$R_{vol}^{m} = \frac{V_{ini}^{m}\left( P_{1},T_{1} \right) + \Delta V^{m}}{V_{ini}^{m}\left( P_{1},T_{1} \right)} = 1 + \epsilon_{V} \tag{A3}$$

where $\Delta V^{m}$ is the volume difference between the final and initial conditions for the phase $m$. For a spherical region, $R_{vol}^{m}$ can be used to calculate the ratio of the radii ($R_{rad}^{m}$) between the final and initial conditions of the $m$^th phase as shown below.

$$R_{rad}^{m} = \left( R_{vol}^{m} \right)^{\frac{1}{3}} \tag{A4}$$

When phases expand/contract in a hydrostatic stress field, the stress field that develops within them is also homogeneous. In that case, all the normal stress components would be equal to the hydrostatic stress and the shear stress components would be zero due to the spherical symmetry. However, if a host-inclusion system experience changes in P-T, an additional strain will develop if there is a mismatch in the volumetric strain between the host and the inclusion. The mismatch between the radii ($\Delta u$) of the two phases can be normalized by the radius $r^{i}$ of the inclusion (in the deformed state) as follows:

$$\small{ \begin{align} \frac{\Delta u}{r^{i}} &= \frac{u^{i} - u^{h}}{r^{i}} = \frac{r^{i} - R^{i} - r^{h} + R^{h}}{r^{i}} \\ &= \frac{r^{i} - r^{h}}{r^{i}} = 1 - \frac{r^{h}}{r^{i}} \leftrightarrow \\ \frac{\Delta u}{r^{i}} &= 1 - \frac{r^{h}/R^{h}}{r^{i}/R^{i}} = 1 - \frac{R_{rad}^{h}}{R_{rad}^{i}} \\ &= 1 - \left( \frac{R_{vol}^{h}}{R_{vol}^{i}} \right)^{\frac{1}{3}} \end{align} } \tag{A5}$$

where the superscripts $i$ and $h$ refer to the inclusion and the host and r, R (without subscripts) are their radii at the deformed and undeformed configurations respectively. We note that at the undeformed configuration $R^{i} = R^{h}$. The quantity $\Delta u/r^{i}$ is defined as positive in extension and it is equal to the exact difference of the circumferential strain at the (deformed) host-inclusion interface ($r = r^{i}$). This choice of strain measure corresponds to the circumferential component of the Almansi strain tensor. For isotropic hyperelastic materials this tensor is energy-conjugated with the Kirchhoff stress tensor ($\widehat{\mathbf{\tau}})$:

$$\widehat{\mathbf{\tau}} = J\mathbf{\sigma} \tag{A6}$$

where $J$ is the volume ratio and $\mathbf{\sigma}$ is the true (Cauchy) stress. Our choice of strain in equation (A5) is motivated by the analytical solution of the true stress in the elastoplastic problem (Appendix F, eqs F9 and F11). In the analytical solution of the elasto-plastic problem under finite strains, it is not possible to obtain analytical expressions for stresses as functions of the initial radius.

APPENDIX B

The Constant Value of Pressure in Linear-Elastic Hosts

In this appendix we will summarize the equations for stress balance and strain compatibility for a host-inclusion system considering linear-elastic and isotropic solids. In a spherical coordinate system ($r,\phi,\theta$) the symmetry of the host/inclusion requires that $\sigma_{\phi\phi} = \sigma_{\theta\theta}$, and that the shear stress is zero ($\sigma_{r\phi} = \sigma_{r\theta} = \sigma_{\phi\theta} = 0$). Therefore the equation of stress balance in the radial direction becomes (Kachanov, 1971, p. 110):

$$\frac{d\sigma_{rr}}{dr} + 2\frac{\sigma_{rr} - \sigma_{\theta\theta}}{r} = 0 \tag{B1}$$

the previous relation applies when the body forces are negligible. The components of the normal (infinitesimal) strains are given below:

$$\begin{align} \epsilon_{rr} &= \frac{du}{dr} \\ \epsilon_{\theta\theta} &= \frac{u}{r} \end{align} \tag{B2}$$

where $u(r)$ is a displacement and $\epsilon_{\phi\phi} = \epsilon_{\theta\theta}$. It can be verified by substitution that the previous strain components satisfy the strain compatibility (continuity) condition (Kachanov, 1971, p. 110):

$$\frac{d\epsilon_{rr}}{dr} + \frac{\epsilon_{\theta\theta} - \epsilon_{rr}}{r} = 0 \tag{B3}$$

For a linear-elastic and isotropic material, the (infinitesimal) strain components are given by the following constitutive relationships:

$$\begin{align} \epsilon_{rr} &= \frac{1}{2G}\sigma_{rr} \\ &\quad + \left( \frac{1}{9K} - \frac{1}{6G} \right)\left( \sigma_{rr} + {2\sigma}_{\theta\theta} \right) \\ \epsilon_{\theta\theta} &= \frac{1}{2G}\sigma_{\theta\theta} \\ &\quad + \left( \frac{1}{9K} - \frac{1}{6G} \right)\left( \sigma_{rr} + {2\sigma}_{\theta\theta} \right) \end{align} \tag{B4}$$

where $K,G$ are the bulk and shear (rigidity) moduli respectively. By replacing equation (B4) into eq (B3) and simplifying the result using eq (B1) we obtain (Lubliner, 2008, p. 221):

$$\frac{d\left( \sigma_{rr} + {2\sigma}_{\theta\theta} \right)}{dr} = 0 \tag{B5}$$

The last result requires that that the quantity $\sigma_{rr} + {2\sigma}_{\theta\theta}$ stays constant in the radial direction. Therefore, we have:

$$\sigma_{rr} = - {2\sigma}_{\theta\theta} + C \tag{B6}$$

where $C$ is a constant to be determined by the boundary conditions. From the definition of pressure as the negative mean stress we finally obtain:

$$P = - \frac{\sigma_{rr} + {2\sigma}_{\theta\theta}}{3} \tag{B7}$$

The last two relations (equations B6 and B7) imply that pressure will be constant within a homogeneous and linear-elastic, isotropic solid.

APPENDIX C

The Analytical Solution for Large Volume Changes with a constant Shear Modulus

Due to the differential expansion/contraction between host and inclusion a strain difference will be developed between the two phases. In this example we will assume that the host is much larger than the inclusion. The difference in circumferential strain ($\Delta\epsilon_{\theta\theta}$) at the host inclusion interface will induce a stress difference ($\Delta\sigma_{ij}$) from the homogeneous state which, in this case, is taken as the stress state of the host at the final stage. In general, the absolute value of the stress difference (not the total stress) will be much smaller than the elastic moduli of the minerals (for example, $\left| \Delta\sigma_{ij} \right| \ll G,K$) and therefore a linear-elastic solution can serve as a good approximation for the calculation of $\Delta\sigma_{jk}$. The complete solution will thus be the sum of a basic homogeneous state at the pressure of the host and a perturbation $\Delta\sigma_{jk}$. However, both the basic state and the perturbation must satisfy the stress balance relations (Appendix B, eq B1).

Furthermore, the stress difference tensor $\Delta\sigma_{jk}$ can be decomposed into a hydrostatic and a deviatoric tensor as shown below:

$$\Delta\sigma_{jk} = - \Delta{P\delta}_{jk} + \Delta\tau_{jk} \tag{C1}$$

where $\delta_{jk}$ is the Kronecker delta, $P$ is pressure (negative mean stress) and $\tau_{jk}$ is the deviatoric stress tensor. The final state of the host is considered to be the basic state and is under hydrostatic stress. Therefore both $\Delta P$ and $\Delta\tau_{jk}$ are zero in the host at infinity. However, due to the result from equations (B6) and (B7) in Appendix B, $\Delta P^{h}$ must remain zero within the host (subscript or superscripts $i,h$ indicate host/inclusion respectively). Strictly speaking, the previous assumption is valid for linear-elastic rheology (see Appendix B). However, even in the case of the fully non-linear elastic solution, the variation of mean stress within the host is negligible and therefore its pressure can be approximated as constant (fig. 5 in the main text). As a consequence, with respect to the host, eq C1 becomes:

$$\Delta\sigma_{jk}^{h} \approx \Delta\tau_{jk}^{h} \tag{C2}$$

Due to its symmetric loading, no deviatoric stress develops within the inclusion ($\Delta\tau_{rr}^{i} = 0$). Therefore eq (C1), with respect to the inclusion, reduces to:

$$\Delta\sigma_{jk}^{i} = - \Delta{P^{i}\delta}_{jk} \tag{C3}$$

By using equations (C2) and (C3), and the condition of normal-stress balance at the host-inclusion interface we obtain:

$$\begin{align} \Delta\sigma_{rr}^{i} &= \Delta\sigma_{rr}^{h} \leftrightarrow \\ \Delta P^{i} &= - \Delta\tau_{rr}^{h} = - \Delta\sigma_{rr}^{h} \end{align} \tag{C4}$$

Using now the definition of infinitesimal strain (Appendix B, eq B2), the components of the stress difference for the host become a function of the strain difference:

$${\Delta\sigma}_{rr}^{h} = 2G^{h}{\Delta\epsilon}_{rr}^{h} \tag{C5a}$$

$${\Delta\sigma}_{\theta\theta}^{h} = 2G^{h}{\Delta\epsilon}_{\theta\theta}^{h} \tag{C5b}$$

Furthermore, due to equation (B6, Appendix B), the two independent stress components are related as follows:

$${\Delta\sigma}_{rr} = - 2{\Delta\sigma}_{\theta\theta} \tag{C6}$$

Following the strain definition as in equation (B2, Appendix B), the difference in the circumferential strain is thus given by:

$$\Delta\epsilon_{\theta\theta} = \frac{\Delta u}{r} \tag{C7}$$

Substitution of eq (C7) into eq (C5b) and replacement of the result into equation (C6) results to the difference of the normal stress at the side of the host:

$$\Delta\sigma_{rr}^{h} = - 4G^{h}\frac{\Delta u^{h}}{r} \tag{C8}$$

Finally, by replacing eq (C4) and eq (A5, Appendix A) in eq (C8) we obtain:

$$\Delta P^{i} = 4G^{h}\left\lbrack 1 - \left( \frac{R_{vol}^{h}}{R_{vol}^{i}} \right)^{\frac{1}{3}} \right\rbrack \tag{C9}$$

Note that, due to the residual pressure difference that develops in the inclusion $R_{vol}^{i}$ and $R_{vol}^{h}$ are calculated at different final conditions, thus, by replacing eq (A2, Appendix A) into eq (C9) we obtain:

$$\scriptsize{ \Delta P^{i} = 4G^{h}\left\lbrack 1 - \left( \frac{V_{fin}^{h}\left( P_{2},T_{2} \right)}{V_{ini}^{h}\left( P_{1},T_{1} \right)} \cdot \frac{V_{ini}^{i}\left( P_{1},T_{1} \right)}{V_{fin}^{i}\left( P_{3},T_{2} \right)} \right)^{\frac{1}{3}} \right\rbrack } \tag{C10}$$

where $P_{1} - T_{1}$ are the initial conditions (host and inclusion), $P_{2} - T_{2}$ are the final conditions of the host and $P_{3}$ is the final pressure of the inclusion given by:

$$P_{3}^{i} = P_{2}^{h} + \Delta P^{i} \tag{C11}$$

APPENDIX D

The Approximation in the Solution of Guiraud and Powell (2006)

In this appendix we demonstrate that the solution of Guiraud and Powell (2006; their eq 1) is a linearized version of our new solution (eq C9, Appendix C). We start by rewriting eq (C9, Appendix C) as follows:

$$\Delta P^{i}\left( R_{vol}^{h} \right) = 4G^{h}\left\lbrack 1 - \left( \frac{R_{vol}^{h}}{R_{vol}^{i}} \right)^{\frac{1}{3}} \right\rbrack \tag{D1}$$

We note that the inclusion pressure difference ($\Delta P^{i}$) is zero only if the volumetric strain of the host and the inclusion are the same ($R_{vol}^{h}/R_{vol}^{i} = 1$). Taking a 1^st-order Taylor expansion of eq (D1) around $R_{vol}^{h} = R_{vol}^{i}$ results to:

$$\small{ \begin{align} \Delta P^{i}\left( R_{vol}^{h} \right) &\approx \left. \ \Delta P^{i}\left( R_{vol}^{h} \right) \right|_{R_{vol}^{h} = R_{vol}^{i}} \\ &\quad + \left. \ \frac{d\Delta P^{i}\left( R_{vol}^{h} \right)}{dR_{vol}^{h}} \right|_{R_{vol}^{h} = R_{vol}^{i}}\left( R_{vol}^{h} - R_{vol}^{i} \right) \end{align} } \tag{D2}$$

By the definition of perturbation $\Delta P^{i}$, the first term on the right-hand side of eq (D2) is identically zero. At the limit of very small deformations, we can approximate $R_{vol}^{i} = R_{vol}^{h} \approx 1$ in the evaluation of the first derivative of equation (D1). Then, the first derivative of the pressure perturbation in eq (D2) becomes:

$$\left. \ \frac{d\Delta P^{i}\left( R_{vol}^{h} \right)}{dR_{vol}^{h}} \right|_{R_{vol}^{h} = R_{vol}^{i}} \approx - \frac{4}{3}G^{h} \tag{D3}$$

Substituting the previous result into eq (D2) we obtain:

$$\Delta P^{i}\left( R_{h}^{vol} \right) \approx - \frac{4}{3}G^{h}\left( R_{vol}^{h} - R_{vol}^{i} \right) \tag{D4}$$

Equation (D4) after rearrangement and replacement of the symbols of the volume ratios becomes:

$$\small{ \frac{V_{fin}^{h}\left( P_{2},T_{2} \right)}{V_{ini}^{h}\left( P_{1},T_{1} \right)} \approx \frac{V_{fin}^{i}\left( P_{3},T_{2} \right)}{V_{ini}^{i}\left( P_{1},T_{1} \right)} - \frac{3}{4G^{h}}\Delta P^{i} } \tag{D5}$$

The previous approximation is the same as in eq 1 from Guiraud and Powell (2006) if one replaces the approximation sign ($\approx$) by the equal sign ($=$). Zhong, Dabrowski, et al. (2020) have suggested an alternative to the previous equation. Using our notation, their equation 7 can be written as:

$$\begin{align} \ln\left( \frac{V_{fin}^{h}\left( P_{2},T_{2} \right)}{V_{ini}^{h}\left( P_{1},T_{1} \right)} \right) &= ln\left( \frac{V_{fin}^{i}\left( P_{3},T_{2} \right)}{V_{ini}^{i}\left( P_{1},T_{1} \right)} \right) \\ &\quad - \frac{3}{4G^{h}}\Delta P^{i} \end{align} \tag{D6}$$

The last form is based on the usage of logarithmic strain as a strain measure to describe the volumetric-strain mismatch between the two phases.

APPENDIX E

Numerical Solution of the Elastoplastic Lamé Problem with Finite Elastic and Plastic Deformations

We use the Lagrangian hyperelastic problem statement in the initial configuration written in an invariant (tensorial) notation and adapted for spherical symmetry (Levin et al., 2016; Levin, Zingerman, et al., 2013; Lurie, 1990). The equation of motion of the deformable solid is written in the coordinate system of the initial (undeformed) state (eq E1):

$$\nabla^{0} \cdot \mathbf{S}_{\mathbf{PK}\mathbf{1}}^{\mathbf{0}} = \rho_{0}\left( \frac{\partial^{2}\mathbf{u}}{\partial t^{2}} + \widehat{d}\frac{\partial\mathbf{u}}{\partial t} \right) \tag{E1}$$

where $\rho_{0}$ is the initial density, $\widehat{d}$ is a damping coefficient, and the dot sign ($\bullet$) is used for a single tensor contraction (colon for double contraction). The Lagrangian (material) displacement vector is $\mathbf{u}$, the gradient operator $\nabla^{0}$ is applied on the coordinates of the initial state and $\mathbf{S}_{\mathbf{PK}\mathbf{1}}^{\mathbf{0}}$ represents the first (non-symmetric) Piola-Kirchhoff stress tensor. The relation of $\mathbf{S}_{\mathbf{PK}\mathbf{1}}^{\mathbf{0}}$ to the true (Cauchy) stress tensor $\boldsymbol{\sigma}$ is given by:

$$\boldsymbol{\sigma} = \frac{1}{J}\mathbf{S}_{\mathbf{PK}\mathbf{1}}^{\mathbf{0}}\mathbf{\cdot}\mathbf{F}^{\mathbf{T}} \tag{E2}$$

where $\mathbf{F}$ is the deformation gradient and $J$ is the relative volume variation as defined previously. $\mathbf{F}$ and $J$ are given by the following relationships:

$$\mathbf{F =}\left( \mathbf{I +}\nabla^{0}\mathbf{u} \right) \tag{E3a}$$

$$J = det\mathbf{F} \tag{E3b}$$

where $\mathbf{I}$ is the identity tensor. At this point we can decompose the full deformation gradient as the product of an elastic ($\mathbf{F}_{\mathbf{e}}$) and plastic ($\mathbf{F}_{\mathbf{p}}$) part:

$$\mathbf{F =}\mathbf{F}_{\mathbf{e}}\mathbf{\cdot}\mathbf{F}_{\mathbf{p}} \tag{E4}$$

In addition, the plastic right Cauchy-Green deformation tensor is given by:

$$\mathbf{C}_{\mathbf{p}}\mathbf{=}\mathbf{F}_{\mathbf{p}}^{\mathbf{T}}\mathbf{\cdot}\mathbf{F}_{\mathbf{p}} \tag{E5}$$

The constitutive relation for a hyperelastic material is given by:

$$\boldsymbol{\sigma}\left( \mathbf{B}_{\mathbf{e}} \right) = \frac{2}{J}\mathbf{B}_{\mathbf{e}}\mathbf{\cdot}\frac{\partial W\mathbf{(}\mathbf{B}_{\mathbf{e}}\mathbf{)}}{\partial\mathbf{B}_{\mathbf{e}}} \tag{E6}$$

where $W\mathbf{(}\mathbf{B}_{\mathbf{e}}\mathbf{)}$ is the strain energy function and $\mathbf{B}_{\mathbf{e}}$ is an elastic Finger deformation tensor. The elastic Finger deformation tensor is given by:

$$\mathbf{B}_{\mathbf{e}}\mathbf{=}\mathbf{F}_{\mathbf{e}}\mathbf{\cdot}\mathbf{F}_{\mathbf{e}}^{\mathbf{T}}\mathbf{= F \cdot}\mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}}\mathbf{\cdot}\mathbf{F}^{\mathbf{T}} \tag{e7}$$

For the case of finite strains, an associative plastic flow rule can be generalized as follows

$$\mathbf{F \cdot}\frac{\partial\mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}}}{\partial t}\mathbf{\cdot}\mathbf{F}^{\mathbf{T}} = -2\dot{\lambda} \frac{\partial Q\left( \boldsymbol{\sigma} \right)}{\mathbf{\partial}\boldsymbol{\sigma}}\mathbf{\cdot B}_{\mathbf{e}} \tag{E8}$$

where $Q\left( \mathbf{\sigma} \right)$ is the plastic potential and $\dot{\lambda}$ is the time derivative of the plastic multiplier. For the case of a non-associative Drucker-Prager model, the plastic yield surface $\Phi\left( \mathbf{\sigma} \right)$ and the plastic potential are given by (Benallal et al., 2008; Coussy, 2003):

$$\begin{align} \Phi\left( \boldsymbol{\sigma} \right) &= \sqrt{\frac{1}{2}\left( \boldsymbol{\sigma -}\frac{\boldsymbol{\sigma:I}}{\mathbf{3}}\mathbf{I} \right):\left( \boldsymbol{\sigma -}\frac{\boldsymbol{\sigma:I}}{\mathbf{3}}\mathbf{I} \right)} \\ &\quad - K_{1} - K_{2}\left( \boldsymbol{\sigma:I} \right) \end{align} \tag{E9a}$$

$$\begin{align} Q\left( \boldsymbol{\sigma} \right) &= \sqrt{\frac{1}{2}\left( \boldsymbol{\sigma -}\frac{\boldsymbol{\sigma:I}}{\mathbf{3}}\mathbf{I} \right):\left( \mathbf{\sigma -}\frac{\boldsymbol{\sigma:I}}{\mathbf{3}}\mathbf{I} \right)} \\ &\quad - C\left( \boldsymbol{\sigma:I} \right) \end{align} \tag{E9b}$$

where $K_{1}$, $K_{2}$ and $C$ are the cohesion coefficient, the coefficient of internal friction and the dilatancy coefficient respectively.

In order to solve a generalized static Lamé problem of a stress concentration in the spherically symmetric solid under internal and external pressures, we use the above dynamic system of PDEs (Zingerman et al., 2016, 2019). We will utilize a dynamic relaxation method with a proper choice of a damping coefficient to converge to a static solution by integrating the corresponding damped dynamic equations. Accordingly, an unknown displacement vector will be computed using the time integration scheme. We will use a classical 2^nd order in time, explicit, Newmark scheme (Levin & Vershinin, 2008; Zienkiewicz & Taylor, 2000). This reads:

$$\mathbf{u}\left( t_{n + 1} \right) = \mathbf{u}_{n + 1}\mathbf{=}\mathbf{u}_{n} + \mathbf{v}_{n}\Delta t + \boldsymbol{\alpha}_{n}\frac{\Delta t^{2}}{2} \tag{E10a}$$

$$\mathbf{v}_{n + 1}\mathbf{=}\mathbf{v}_{n}(1 - \beta)\boldsymbol{\alpha}_{n}\Delta t + \beta\boldsymbol{\alpha}_{n + 1}\Delta t \tag{E10b}$$

where $\mathbf{v}_{n}\mathbf{,}\mathbf{\alpha}_{n}$ are the velocity and the acceleration vectors for the $n$^th timestep and $\beta$ is a numerical parameter. This scheme is conditionally stable (according to the Courant’s condition) when $\beta > 0.5$. At this point, the elastic Finger deformation tensor ($\mathbf{B}_{e}$, eq E7) for the $(n + 1)^{th}$ timestep is given by:

$$\begin{align} \mathbf{B}_{e}^{\mathbf{n + 1}}&\mathbf{=}\mathbf{F}_{n + 1}\mathbf{\cdot}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n + 1}\mathbf{\cdot}\mathbf{F}_{n + 1}^{\mathbf{T}}\\ &\mathbf{=}\mathbf{F}_{n + 1}\mathbf{\cdot}\left\lbrack \left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n}\mathbf{+ \mathrm{\Delta}}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right) \right\rbrack\\ &\quad \mathbf{\cdot}\mathbf{F}_{n + 1}^{\mathbf{T}} \end{align} \tag{E11}$$

where $\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n}$ is the accumulated inverse plastic right Cauchy-Green deformation tensor at the $n$ previous steps. For the $(n + 1)^{th}$ timestep the generalized plastic flow rule (eq E8) can be written as:

$$\small{ \begin{align} \mathbf{F}_{n + 1}\mathbf{\cdot \mathrm{\Delta}}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)\mathbf{\cdot}\mathbf{F}_{n + 1}^{\mathbf{T}} &= - 2\mathbf{\mathrm{\Delta}}\lambda\left. \ \frac{\partial Q\left( \boldsymbol{\sigma} \right)}{\partial\boldsymbol{\sigma}} \right|_{n + 1} \\ &\quad \cdot \mathbf{B}_{e}^{\mathbf{n + 1}} \end{align} } \tag{E12}$$

By substituting equation (E12) into equation (E11) and using equation (E3) and $\mathbf{u}\nabla^{0}\mathbf{=}\left( \nabla^{0}\mathbf{u} \right)^{T}$ we obtain:

$$\small{ \begin{align} \mathbf{B}_{e}^{\mathbf{n + 1}}&\mathbf{=}\left( \mathbf{I +}{\mathbf{u}_{n + 1}\nabla}^{0} \right)\mathbf{\cdot}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n}\mathbf{\cdot}\left( \mathbf{I +}\nabla^{0}\mathbf{u}_{n + 1} \right) \\ &\quad- 2\mathbf{\mathrm{\Delta}}\lambda\left. \ \frac{\partial Q\left( \boldsymbol{\sigma} \right)}{\partial\boldsymbol{\sigma}} \right|_{n + 1} \cdot \mathbf{B}_{e}^{\mathbf{n + 1}} \end{align} } \tag{E13}$$

which becomes:

$$\small{ \begin{align} \mathbf{B}_{e}^{\mathbf{n + 1}}&\mathbf{=}\left( \mathbf{I} + 2\mathbf{\mathrm{\Delta}}\lambda\left. \ \frac{\partial Q\left( \boldsymbol{\sigma} \right)}{\partial\boldsymbol{\sigma}} \right|_{n + 1} \right)^{- 1}\left( \mathbf{I +}{\mathbf{u}_{n + 1}\nabla}^{0} \right)\\ &\quad \mathbf{\cdot}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n}\mathbf{\cdot}\left( \mathbf{I +}\nabla^{0}\mathbf{u}_{n + 1} \right) \end{align} } \tag{E14}$$

where $\mathbf{\mathrm{\Delta}}\lambda$ is found from the plastic yield condition $\Phi\left( \mathbf{\sigma}\left( \mathbf{B}_{e}^{\mathbf{n + 1}} \right) \right) = 0$.

Thus, we obtain the following system of nonlinear algebraic equations (eqs E15). These equations need to be solved at each integration step and for every material point of the deformable solid in order to account for finite plastic deformations:

$$\small{ \begin{align} \mathbf{B}_{e}^{\mathbf{n + 1}}&\mathbf{=}\left( \mathbf{I} + 2\mathbf{\mathrm{\Delta}}\lambda\left. \ \frac{\partial Q\left( \boldsymbol{\sigma} \right)}{\partial\boldsymbol{\sigma}} \right|_{n + 1} \right)^{- 1}\left( \mathbf{I +}{\mathbf{u}_{n + 1}\nabla}^{0} \right)\\ &\quad \mathbf{\cdot}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n}\mathbf{\cdot}\left( \mathbf{I +}\nabla^{0}\mathbf{u}_{n + 1} \right) \end{align} } \tag{E15a}$$

$$\small{ \begin{align} \boldsymbol{\sigma}\left( \mathbf{B}_{e}^{\mathbf{n + 1}} \right) &= \boldsymbol{\sigma}_{n + 1} \\ &= \frac{2}{\det\left( \mathbf{I +}\nabla^{0}\mathbf{u}_{n + 1} \right)}\mathbf{B}_{e}^{\mathbf{n + 1}}\\ &\quad \mathbf{\cdot}\left. \ \frac{\partial W\left( \mathbf{B}_{\mathbf{e}} \right)}{\partial\mathbf{B}_{\mathbf{e}}} \right|_{n\mathbf{+}1} \end{align} } \tag{E15b}$$

$$\Phi\biggl( \boldsymbol{\sigma}\left( \mathbf{B}_{e}^{\mathbf{n + 1}} \right) \biggr) = 0 \tag{E15c}$$

Solving this system of equations using any nonlinear iterative scheme (Bakhvalov et al., 2008) we obtain $\mathbf{\sigma}_{n + 1}$ and $\mathbf{\mathrm{\Delta}}\lambda$ and also the updated inverse of the plastic right Cauchy-Green deformation tensor $\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n + 1}\mathbf{=}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)_{n}\mathbf{+ \mathrm{\Delta}}\left( \mathbf{C}_{\mathbf{p}}^{\mathbf{- 1}} \right)$. Finally, the unknown acceleration $\mathbf{\alpha}_{n + 1}$ is obtained by solving the following dynamic equation:

$$\nabla^{0} \cdot \left( \mathbf{S}_{\mathbf{PK}\mathbf{1}}^{\mathbf{0}} \right)_{n + 1} = \rho_{0}\left( \boldsymbol{\alpha}_{n + 1} + \widehat{d}\mathbf{v}_{n + 1} \right) \tag{E16}$$

In order to solve the PDE in space accurately, we will apply spectral element method (FIDESYS, 2022; Karpenko et al., 2016; Konovalov et al., 2017) using high order basis functions. The corresponding Galerkin weak formulation of the above PDE produces the following system of linear algebraic equations with respect to $\mathbf{\alpha}_{n + 1}$ (Levin et al., 2016; Zienkiewicz & Taylor, 2000):

$$\small{ \mathbf{M} \cdot \boldsymbol{\alpha}_{n + 1} + \mathbf{C} \cdot \mathbf{v}_{n + 1} + \mathbf{K}\left( \mathbf{u}_{n + 1} \right) - \mathbf{F} = 0 } \tag{E17}$$

where $\mathbf{M}$ is the mass matrix, $\mathbf{C}$ is a damping matrix, $\mathbf{K}$ is the vector of internal forces, $\mathbf{F}$ is the external load and $\mathbf{N}$ is the vector of spectral element basis functions. $\mathbf{M}$, $\mathbf{C}$, K, and $\mathbf{F}$ are given as follows:

$$\mathbf{M} = \int_{\Omega}^{}{\mathbf{N}^{T}\rho_{0}\mathbf{N}d\Omega} \tag{E18a}$$

$$\mathbf{C} = \int_{\Omega}^{}{\mathbf{N}^{T}\rho_{0}\widehat{d}\mathbf{N}d\Omega} \tag{E18b}$$

$$\mathbf{K}\left( \mathbf{u} \right) = \int_{\Omega}^{}{\left( \mathbf{S}_{\mathbf{PK}\mathbf{1}}^{\mathbf{0}} \right)_{n + 1}\left( \nabla\mathbf{u}_{n + 1} \right) \cdot \nabla\mathbf{N}d\Omega} \tag{E18c}$$

$$\mathbf{F =}\oint_{\mathbf{\Gamma}}^{}{\mathbf{N}^{\mathbf{T}}\boldsymbol{\sigma}_{n}d\Gamma} \tag{E18d}$$

Thanks to the distinctive feature of a spectral element method (Charara et al., 2011) the mass matrix (and a damping matrix correspondingly) is diagonal so we obtain values of $\boldsymbol{\alpha}_{n + 1}$ explicitly using the vectors $\mathbf{u}_{n},\mathbf{v}_{n},\mathbf{a}_{n}$ from the previous time step.

APPENDIX F

Analytical Solution of the Elastoplastic Lamé Problem with Finite Elastic and Plastic Deformations

The statement of the hollow-sphere problem in the coordinates of the final state includes the following equilibrium equation (see also eq B1, Appendix B).

$$\frac{d\sigma_{rr}}{dr} + \frac{2\left( \sigma_{rr} - \sigma_{\phi\phi} \right)}{r} = 0 \tag{F1}$$

The stress components can be written as functions of the stretches ($\lambda_{r,\phi,\theta}$) along the principal strain directions (Levin et al., 2021, p. 3):

$$\begin{align} \sigma_{rr} &= 2\mu\left\lbrack \left( \lambda_{\phi}^{e} \right)^{- 2} - J_{e}^{- 2/3} \right\rbrack \\ &\quad + \frac{K^{0}}{K^{'}}\left\lbrack 1 - J_{e}^{- K^{'}} \right\rbrack \\ \sigma_{\phi\phi} &= 2\mu\left\lbrack \left( \lambda_{r}^{e}\lambda_{\phi}^{e} \right)^{- 1} - J_{e}^{- 2/3} \right\rbrack \\ &\quad + \frac{K^{0}}{K^{'}}\left\lbrack 1 - J_{e}^{- K^{'}} \right\rbrack \end{align} \tag{F2}$$

where $J_{e} = \lambda_{r}^{e}\left( \lambda_{\phi}^{e} \right)^{2}$ is equal to the volume ratio (eq A2, Appendix A). By defining $R$ and $r$ as the radial coordinates of the particle in the initial (undeformed) and final (deformed) states, the kinematic relations become:

$$\lambda_{r} = \left( \frac{dR}{dr} \right)^{- 1},\ \ \lambda_{\phi} = \frac{r}{R} \tag{F3}$$

and

$$\lambda_{r} = \lambda_{r}^{e}\lambda_{r}^{p},\ \ \ \lambda_{\phi} = \lambda_{\phi}^{e}\lambda_{\phi}^{p} \tag{F4}$$

where the superscripts $e,p$ indicate elastic and plastic strains respectively.

Upon yielding, the Drucker-Prager plasticity condition (eq E9a) reads

$$\small{ \frac{\sigma_{\phi\phi} - \sigma_{rr}}{\sqrt{3}} - K_{1} - K_{2}\left( \sigma_{rr} + 2\sigma_{\phi\phi} \right) = 0 } \tag{F5}$$

where $K_{1}$ and $K_{2}$ are material parameters. Due to the spherical symmetry of the problem, the plastic flow law (eq E8, taking into account E9b) can be transformed as:

$$\frac{dv}{dr} + 2\gamma\frac{v}{r} = \frac{{\dot{\lambda}}_{r}^{e}}{\lambda_{r}^{e}} + 2\gamma\frac{{\dot{\lambda}}_{\phi}^{e}}{\lambda_{\phi}^{e}} \tag{F6}$$

where $v = v(r)$ is the plastic deformation rate in the radial direction and $\gamma = \frac{\sqrt{3} + C}{\sqrt{3} - 2C}$ where $C$ is a material constant (eq E9b). The boundary conditions are:

$$\begin{align} \left. \ \sigma_{rr} \right|_{r = a} &= - P_{a} \\ \left. \ \sigma_{rr} \right|_{r = b} &= 0 \end{align} \tag{F7}$$

where $a$ and $b$ are the inner and outer radii of a hollow sphere in a deformed state, and $P_{a}$ is the pressure applied to the inner boundary of the sphere. Using the method proposed by Carroll (1988), Levin et al. (2021) solved the elastic hollow-sphere problem. The solution has the form

$$r^{3} = AR^{3} + B \tag{F8}$$

where $A$ and $B$ are constants that are determined from the boundary conditions (eq F7). The approach suggested by Levin et al. (2021), allows the determination of these constants when the inner and outer radii are known in either the deformed ($a,b$) or the undeformed ($a_{0},b_{0}$) state. Based on eq (F8), one can find the multiplicities of the elongations (eq F3) and, in addition, the stresses can be evaluated using the formulas in eq (F2).

In order to solve elastoplastic problem, we follow the approach proposed by Hill (1950). This approach is generalized to the case when not only plastic but also elastic deformations are considered finite. However, instead of the von Mises plasticity condition, for which the solution was obtained in Hill’s (1950) work, the Drucker-Prager condition (eq F5) and the plastic flow law (eq F6) are used here. To determine the pressure at which plastic deformation begins, the boundary condition on the inner boundary of the elastic problem (eq F7) is replaced by the condition given in eq (F5) at $r = a$. Furthermore, the solution is found as a function of the parameter $c$ which represents the radius of the plastic region. To find a solution in the elastic region $c\ < r\ < b$, the boundary condition that is applied on the inner boundary (at $r = a$; eq F7) is replaced by the condition given in eq (F5) at $r\ = \ c$. In particular, the pressure $P_{c}$ at the boundary of the plastic region ($r\ = \ c$) and the multiplicity of elongations at this boundary are determined. These quantities are used further to find a solution in the plastic region.

To determine the stresses in the plastic region, the equilibrium equation (eq F1) and the plasticity condition (eq F5) are simultaneously solved. This condition is represented as

$$\sigma_{\phi\phi} - \sigma_{rr} = M + N\sigma_{rr}\ \tag{F9}$$

where $M = \frac{3K_{1}}{\sqrt{3} - 6K_{2}}$ and $N = \frac{9K_{2}}{\sqrt{3} - 6K_{2}}$.

Substitution of equation (F9) into equation (F1) yields

$$\frac{d\sigma_{rr}}{dr} - \frac{2{(M + N\sigma}_{rr})}{r} = 0\ \tag{F10}$$

This equation (eq F10) is solved under the condition $\left. \ \sigma_{r} \right|_{r = c} = - P_{c}$. The solution has the form

$$\sigma_{rr} = - \frac{M}{N} - \left( P_{c} - \frac{M}{N} \right)\left( \frac{r}{c} \right)^{2N} \tag{F11}$$

And the remaining stress $\sigma_{\phi\phi}$ can be obtained by equation (F9).

To determine the plastic deformations, equation (E6) is solved, in which, by the approach of Hill (1950), the radius $c$ of the plastic region is chosen the variable that quantifies the extent of loading. Moreover, the derivatives ${\dot{\lambda}}_{r}^{e}$ and ${\dot{\lambda}}_{\phi}^{e}$ are represented as

$$\begin{align} {\dot{\lambda}}_{r}^{e} &= \frac{d\lambda_{r}^{e}}{dc} + v(r,c)\frac{d\lambda_{r}^{e}}{dr} \\ {\dot{\lambda}}_{\phi}^{e} &= \frac{d\lambda_{\varphi}^{e}}{dc} + v(r,c)\frac{d{\dot{\lambda}}_{\phi}^{e}}{dr} \end{align} \tag{F12}$$

In the following part we can proceed in solving equation (F6) analytically by adopting some simplifying assumptions. The expressions for $\lambda_{r}^{e}$ and $\lambda_{\phi}^{e}$ in the plastic region can be represented as

$$\begin{align} \lambda_{r}^{e}(r,c) &= \lambda_{r}^{e}(c,c) + {\Delta\lambda}_{r}^{e}(r,c) \\ \lambda_{\phi}^{e}(r,c) &= \lambda_{\phi}^{e}(c,c) + {\Delta\lambda}_{\phi}^{e}(r,c) \end{align} \tag{F13}$$

It is believed that the increments of the principal elongations ${\Delta\lambda}_{r}^{e}(r,c)$ and ${\Delta\lambda}_{\varphi}^{e}(r,c)$ in the plastic region can be associated with the increments of stresses ${\Delta\sigma}_{rr}(r,c) = \sigma_{rr}(r,c) - \sigma_{rr}(c,c)$ and ${\Delta\sigma}_{\phi}(r,c) = \sigma_{\phi}(r,c) - \sigma_{\phi}(c,c)$ , and, by using linear elasticity we can approximately replace the constitutive relations (eq F2) by the following forms

$$\small{ \begin{align} {\Delta\sigma}_{rr}(r,c) &= \left( K_{0} - \frac{2}{3}\mu \right)\left( {\Delta\lambda}_{r}^{e}(r,c) + 2{\Delta\lambda}_{\phi}^{e}(r,c) \right) \\ &\quad + 2\mu{\Delta\lambda}_{r}^{e}(r,c) \\ {\Delta\sigma}_{\phi\phi}(r,c) &= \left( K_{0} - \frac{2}{3}\mu \right)\left( {\Delta\lambda}_{r}^{e}(r,c) + 2{\Delta\lambda}_{\phi}^{e}(r,c) \right) \\ &\quad + 2\mu{\Delta\lambda}_{\varphi}^{e}(r,c) \end{align} } \tag{F14}$$

We can thus express equations (F14) with respect to ${\Delta\lambda}_{r}^{e}(r,c)$ and ${\Delta\lambda}_{\phi}^{e}(r,c)$ and substitute the result into equations (F13). The previous result can be substituted into equations (F12) and into the right-hand side of equation (F6). When calculating the denominators of the fractions in the right-hand side of equation (F6), the following assumptions are used

$$\begin{align} \lambda_{r}^{e}(r,c) &\approx \lambda_{r}^{e}(c,c) \\ \lambda_{\phi}^{e}(r,c) &\approx \lambda_{\phi}^{e}(c,c) \end{align} \tag{F15}$$

Thus, equation (F6) can be reduced to the following form

$$\begin{align} \frac{dv(r,c)}{dr} + 2\gamma\frac{v(r,c)}{r} &= Q + Sr^{2N} \\ &\quad+ Tv(r,c)r^{2N - 1} \end{align} \tag{F16}$$

where $Q$, $S$, and $T$ are coefficients that depend on $c$. This equation can be solved analytically using symbolic algebra tools. As a result, the rate of plastic deformation $v(r,\ c)$ is determined. An explicit expression for this velocity is cumbersome and is not presented here. At the final stage, the differential equation is solved numerically (by using Euler’s method for example)

$$\frac{da}{dc} = v(a,c) \tag{F17}$$

and the radius $a$ of the cavity in the deformed state is determined as a function of $c$.