Calcite Dissolution-Reprecipitation Reactions Are a Key Control on the Sr/Ca, Mg/Ca and δ^88/86Sr Compositions of Himalayan River Waters

1. INTRODUCTION

The processes which control global climate on long timescales play a critical role in the evolution of our planet, yet the feedbacks which have kept the surface of the Earth habitable are not well understood (e.g., Berner et al., 1983; Chamberlin, 1898; Coogan & Dosso, 2015; Sleep & Zahnle, 2001; Walker et al., 1981). The marked global cooling over the last 50 million years should provide an accessible record of the processes responsible and consequently much attention has been paid to the potential impact of the exhumation of the Himalayas cooling climate through the increased ‘weatherability’ of rapidly eroding crust (e.g., Kump et al., 2000; Ruddiman, 1997). However, the difficulties in deconvolving the dissolved chemical fluxes from the Himalayan-Tibetan orogen into components derived from silicate mineral weathering by carbonic acid (which impacts long-term climate), carbonate mineral weathering by carbonic acid (which is climate-neutral in the long term), and sulphuric acid weathering (which may release CO₂), frustrates attempts to evaluate the potential impact of the orogen on climate (e.g., Bickle et al., 2015; English et al., 2000; Galy & France-Lanord, 1999; Harris et al., 1998; Krishnaswami & Singh, 1998; Tipper, Bickle, et al., 2006; Torres et al., 2014).

The systematics of carbonate weathering in the Himalayas has attracted much attention. The hypothesis that Himalayan carbonate ⁸⁷Sr/⁸⁶Sr ratios were elevated by metamorphic exchange with old silicate minerals (e.g., Palmer & Edmond, 1992; Quade et al., 1997) was verified by Bickle et al. (2001). This contributes to the high ⁸⁷Sr/⁸⁶Sr ratios of the Himalayan riverine discharge which is thought largely responsible for the marked rise in seawater ⁸⁷Sr/⁸⁶Sr ratios over the last 40 Ma (e.g., Edmond, 1992; Galy et al., 1999; Palmer & Edmond, 1992; Richter et al., 1992). A second distinctive characteristic of Himalayan rivers is that their Sr/Ca and Mg/Ca ratios are elevated well above those of their source bedrocks. This is ascribed to precipitation of secondary calcite with low Sr/Ca and Mg/Ca ratios in the river catchments (e.g., Bickle et al., 2015; Chen et al., 2022; English et al., 2000; Galy et al., 1999; Jacobson et al., 2002; Li et al., 2023; Tipper, Galy, et al., 2006). The lack of alternative sources with high Sr/Ca and Mg/Ca ratios, the observation that many Himalayan rivers are saturated or super-saturated in calcite and the presence of travertines in Himalayan catchments are all consistent with this hypothesis (see discussion in Jacobson et al., 2002). The precipitation of secondary calcite impacts the calculation of the fractions of Sr, Ca and Mg derived from silicate and carbonate mineral weathering (e.g., Bickle et al., 2015; Galy et al., 1999; Jacobson et al., 2002; Krishnaswami & Singh, 1998; Singh et al., 1998).

In this paper we use the mass-dependent fractionation of the stable isotopes of strontium, ⁸⁸Sr and ⁸⁶Sr, reported as δ^88/86Sr (δ^88/86Sr = ((⁸⁸Sr/​⁸⁶Sr)_SAMP/​(⁸⁸Sr/​⁸⁶Sr)_NBS987)-​1)x​1000) to investigate lithological control on the riverine δ^88/86Sr ratios as well as carbonate weathering systematics along with previous analyses of Ca-isotopic compositions (Tipper et al., 2008; Tipper, Galy, et al., 2006) from the same regions. δ^88/86Sr data are presented for waters and bedload from rivers draining carbonate-dominated, silicate-dominated and mixed catchments in the Nepalese Himalayas using samples previously analyzed for major and trace cations, anions, ⁸⁷Sr/⁸⁶Sr ratios and lithium isotopic ratios (Bickle et al., 2015; Kisakürek et al., 2005).

Figure 1.Ranges of published modern δ^88/86Sr values (sources in Supplementary material, S1). Note the offset between terrestrial carbonates (carbonates precipitated on the continents) and river waters. Black lines are data means. Data from Himalayan catchments from this work (table 1).

Stable Sr isotopic values have widely been used in the study of chemical weathering processes (e.g., Andrews et al., 2016; Andrews & Jacobson, 2018; Bouchez & von Blanckenburg, 2021; Bullen & Chadwick, 2016; Chao et al., 2015; Stevenson et al., 2016; Wei et al., 2013) (fig. 1). One of the key controls on natural waters was proposed to be the solution of different minerals with distinct δ^88/86Sr values in variable proportions (Andrews & Jacobson, 2018; Chao et al., 2015). de Souza et al. (2010), Andrews et al. (2016) and Bouchez and von Blanckenburg (2021) suggested that biomass uptake might elevate dissolved δ^88/86Sr values. Wei et al. (2013) observed a large seasonal variation in the Xijiang river (δ^88/86Sr from 0.66 ‰ to 0.15 ‰) with the shift to lower δ^88/86Sr values explained as due to increased carbonate input, (see Wu et al., 2024 for a recent review).

Here we show that the δ^88/86Sr values of waters from carbonate-rich catchments tend to be lower than those from silicate-dominated catchments. However, the loss of Ca to secondary calcite in Himalayan river waters may fractionate δ^88/86Sr values. Calcite exhibits precipitation-rate dependent fractionation of ⁸⁸Sr/⁸⁶Sr ratios (AlKhatib & Eisenhauer, 2017; Böhm et al., 2012). Shalev et al. (2017) estimated that precipitation of secondary calcites elevated the mean δ^88/86Sr of global rivers by ~ 0.1‰. Stevenson et al. (2016) suggested that preferential uptake of low δ^88/86Sr by precipitation of Fe-oxyhydroxides and clay minerals elevated dissolved δ^88/86Sr in glacial meltwaters. It is important to understand how isotopic fractionations associated with precipitation of secondary minerals alter δ^88/86Sr values to interpret river water compositions. In this paper the correlation between the δ^88/86Sr and Sr/Ca ratios in samples from a carbonate-dominated catchment is used to place constraints on the mechanisms of carbonate weathering in these Himalayan catchments as well as on the magnitudes and formation rates of the secondary calcite.

2. STUDY AREAS

A range of samples from large and small rivers (main stem and tributaries) were analyzed from sample suites collected in the Nepalese Himalaya (fig. 2). The water samples were collected by Kisakürek et al. (2005) and bed-load sediments by Tipper, Bickle et al. (2006), Tipper, Galy et al. (2006), Tipper et al. (2008), and Bickle et al. (2015). Samples are representative of both carbonate and silicate lithologies at high (2000 to 4000 m) and low (550 to 1300 m) altitudes (table 1) and were collected both before and in the late monsoon. The samples are from the three main lithotectonic units of the Himalayas, the Tibetan Sedimentary Series (TSS), the High Himalayan Crystalline Series (HHCS) and Lesser Himalayan Series (LHS).

2.1. Tibetan Sedimentary Series (TSS)

The tributaries of the upper Marsyandi and Modi Khola (fig. 2) drain Tibetan Sedimentary Series rocks outcropping at altitudes of 3000 to 6000 m on the southern margin of the Tibetan plateau. Erosion rates are ~ 1 mm/yr (Gabet et al., 2008; Godard et al., 2012), monsoonal precipitation < 0.5 m/yr (Burbank et al., 2003) and the area is sparsely vegetated. The TSS consists of limestones, impure limestones and siliclastic sedimentary rocks with pyritic black shales. Metamorphic grades are mainly sub-greenschist facies, but higher grade calc-silicates are exposed in the eastern part of the Marsyandi catchment adjacent to the South Tibetan Detachment Surface (Bordet et al., 1971; Schneider & Masch, 1993; Searle & Godin, 2003). Searle and Godin (2003) assign the calc-silicate unit to the High Himalayan Crystalline Series (fig. 2). No evaporites, in particular gypsum, have been reported in the Marsyandi basin (Bordet et al., 1975).

Figure 2.A) Geology and catchments sampled in the Nepalese Himalaya, modified after Kisakürek et al. (2005) and Parsons et al. (2016) with: I) Marsyandi and its tributaries; (II) Indrawati and its tributaries; (III) Bhoti Kosi and its tributaries; (IV) Dudh Kosi and its tributaries. Location of samples given in table S1 supplementary information. B) Geology and sample localities in the Marsyandi and Modi Khola catchments with the base of the TSS defined by the STDS and the Deurali-Chame detachment within the HHCS after Searle and Godin (2003). Bedload samples have prefix BCT or ETT and dissolved load samples have prefix S or A.

2.2. The High Himalayan Crystalline Series (HHCS)

The High Himalayan Crystalline Series underlies the highest, partly glaciated, steepest and most rapidly eroding terrain with erosion rates ~ 3 mm/yr (West et al., 2015). The climate is Alpine with the monsoonal precipitation up to 4 m/yr. The samples were collected from tributaries of the Dudh Kosi, eastern Nepal, at altitudes of 2500 to 4000 m and from tributaries of the Indrawati, central Nepal, at altitudes of 800 to 1000 m where erosion rates are lower (~ 1 mm/yr, West et al., 2015) (fig. 1). Both catchments contain kyanite and some sillimanite-bearing metapelitic schists and gneisses (Formation I of Le Fort, 1975). In the Marsyandi catchment the two lowest samples from the Dudh Khola and Dana Khola (S22, S24) drain rocks from the High Himalayan Crystalline Series which here comprise calc-silicates containing diopside, amphibole, quartz and calcite bearing assemblages (Formation II), an augen gneiss unit (Formation III) and the Manaslu leucogranite (Le Fort, 1975).

2.3. Lesser Himalayan Series (LHS)

The Lesser Himalayan Series occupies terrain mainly below ~ 3000 m in altitude. The catchments are often densely forested with significant terracing for agriculture. Erosion rates are lower (~ 1 mm/yr, Godard et al., 2012; Vance et al., 2003) and precipitation ~ 2 m/yr. The samples are from tributaries of the Bhoti Kosi (fig. 1) where the LHS contains low grade abundant and often impure dolomites and limestones together with slates, quartzites and phyllites at altitudes of between 800 to 1300 m.

3. MATERIALS AND METHODS

The river waters above were sub-sampled from a suite of preserved (filtered and acidified to pH <2) water samples collected by Kisakürek et al. (2005) (see table S1 in supplementary information). Bedload samples from the Marsyandi River collected by Tipper, Bickle et al. (2006) and Bickle et al. (2015) were dried and powdered in a steel jaw crusher and an agate ball mill (Bickle et al., 2015). For the analyses of whole bed-load samples 10 mg was subject to hot plate dissolution using trace grade HF and HNO₃ acids (Stevenson et al., 2016).

The first batch of stable strontium isotope measurements (tables 1 & 2) was carried out on a Thermo-Finnigan Triton Thermal Ionisation Mass Spectrometer at the University of Durham as described by Stevenson et al. (2014). Two aliquots of each sample (dissolved load or bedload) containing 500 ng of Sr were dried, re-dissolved in 1mL 2.0 M HNO₃ and one aliquot was spiked with an ⁸⁷Sr-⁸⁴Sr double spike (Pearce et al., 2015; Stevenson et al., 2014, 2016). The procedural Sr blank was less than ~ 30 pg, constituting less than 0.1 % of the total Sr analyzed. The isotope data were deconvolved from the spiked and un-spiked analyses using an exponential fractionation law and a Newton-Raphson iterative technique (Albarède & Beard, 2004). The internal precision on the ⁸⁸Sr/⁸⁶Sr isotope ratio varied between ± 7 to ± 15 ppm. The external reproducibility of SRM987 ⁸⁷Sr/⁸⁶Sr ratio normalised to ⁸⁶Sr/⁸⁸Sr = 0.1194 was 0.710226 ± 0.000006 (2σ, ± 8.4 ppm, n = 33). Repeat measurements of IAPSO seawater standard gave δ^88/86Sr values of +0.38 ± 0.03‰ (2σ n = 8) identical to those of de Souza et al. (2010), Fietzke and Eisenhauer (2006), and Krabbenhöft et al. (2010). BCR-2 gave a δ^88/86Sr value of +0.28 ± 0.05‰ (2σ, n=3), indistinguishable from the values of Ma et al. (2013) and Moynier et al. (2010).

The second batch of strontium isotope measurements on the bed load acetic acid leaches (table 2) was carried out on a Neptune Plus multicollector-ICP-mass spectrometer (Thermo Scientific) at the University of Cambridge. Samples and standards were doped with zirconium in the concentration ratio 2:1. Mass bias was estimated from the drift in the ⁹²Zr/⁹⁰Zr and ⁸⁸Sr/⁸⁶Sr ratios and corrected for using an exponential normalisation following Xu et al. (2020). The IAPSO seawater standard gave an ⁸⁷Sr/⁸⁶Sr ratio of 0.709200 ± 19 and an δ^88/86Sr value of +0.389 ± 0.037‰ (2σ on 4 repeats) and Hastings seawater (a Cambridge internal seawater standard) an ⁸⁷Sr/⁸⁶Sr ratio of 0.709188 ± 26 and an δ^88/86Sr value of +0.391 ± 0.027 ‰ (2σ on 9) (together, all the seawater values gave δ^88/86Sr = 0.390 ± 0.029‰ (2σ, n= 13, our best estimate of external reproducibility, table S2 in supplementary information). Standard BHVO2 gave an ⁸⁷Sr/⁸⁶Sr ratio of 0.703500 ± 65, within error of 0.703479 ± 20 (Weis et al., 2006), and an δ^88/86Sr value of 0.25 ± 0.055 ‰ (2se internal errors, n=1), within error of 0.267 ± 0.010 (Klaver et al., 2020). Sr/Ca ratios and Sr contents of the carbonate fraction of bedload samples (table 2) were measured by leaching in cold 10% acetic acid for 8 hours and analyzed by inductively coupled plasma optical emission spectroscopy using synthetic standards similar in composition to the leaches. Additional elements analyzed (Ca, K, Mg, Na, Sr) are listed in table S3 in the supplementary information.

The water cation concentrations from Kisakürek et al. (2005) (table S1 Supplementary Information) are corrected for precipitation and hot spring inputs after Bickle et al. (2015). As noted previously by Bickle et al. (2015), corrections for Na are ~ 25% and the other major cations less than ~12%. For the Marsyandi, Modi Khola and Bhote Kosi catchments the fraction of Sr from precipitation and hot springs averages 3.4% (range 0 to 9%) and the impact on δ^88/86Sr values is unlikely to be significant unless the hot springs have δ^88/86Sr values well outside the range of any terrestrial samples. The water samples from the HHCS Formation I have lower Sr concentrations and higher Cl concentrations resulting in higher Sr fractions apparently derived from precipitation and hot springs (averaging 25% and in sample S4 estimated at greater than 100%). There is considerable scatter in both the available major ion analyses of Himalayan precipitation (Galy & France-Lanord, 1999) and the hot spring compositions (Becker et al., 2008; Evans et al., 2004). The larger corrections to Sr are therefore uncertain and δ^88/86Sr ratios have not been analyzed in either the local precipitation or hot springs. The samples from the Dudh Kosi and Indrawati exhibit no significant correlation between δ^88/86Sr values and the estimated fraction of Sr from precipitation and hot springs suggesting that rain and hot spring inputs have δ^88/86Sr values within the range of the water samples.

4. RESULTS

4.1. Tibetan Sedimentary Series (TSS)

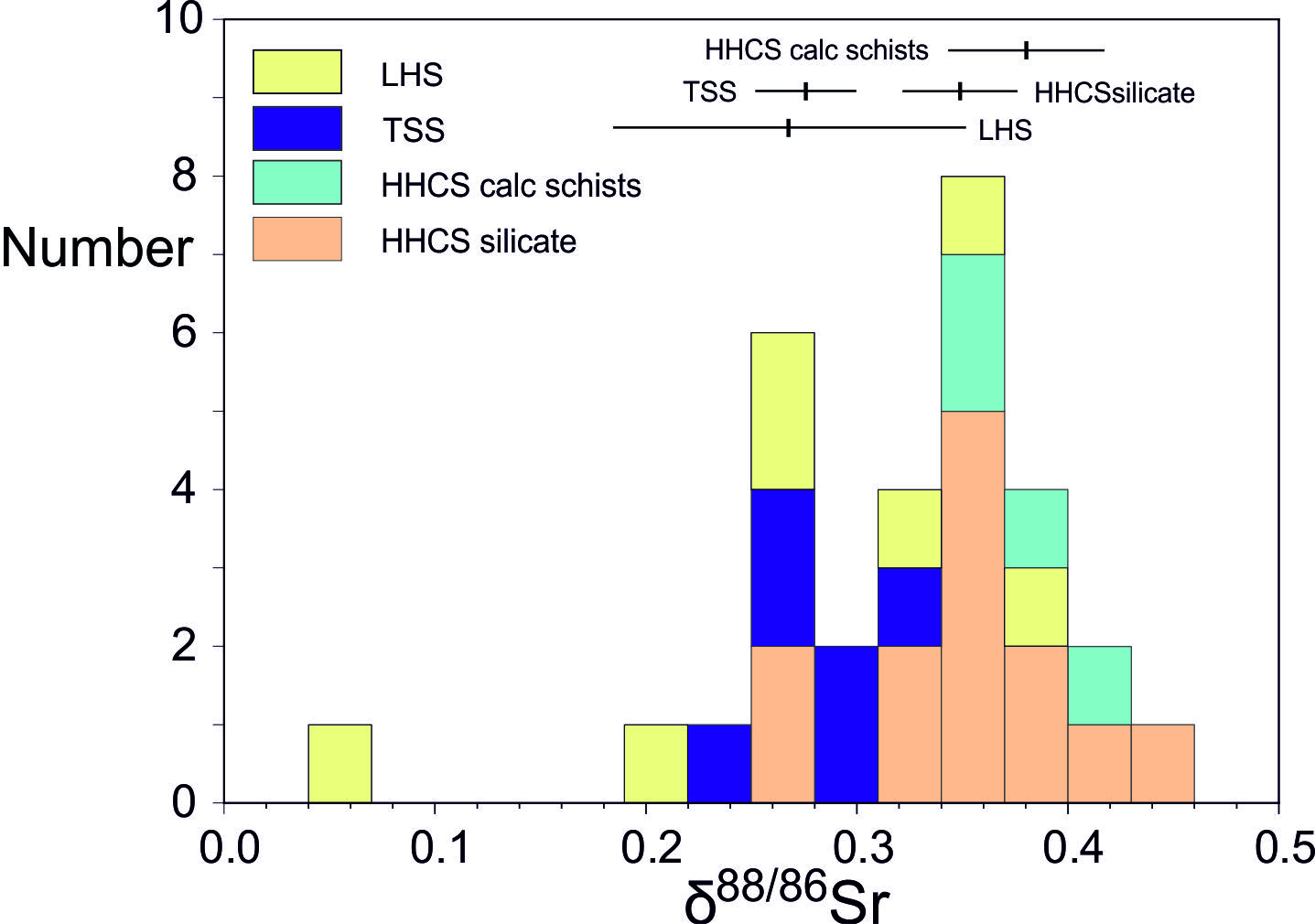
The TSS samples analyzed for δ^88/86Sr were collected in the pre-monsoon from tributaries to Marsyandi between 3200 and 3950 m (samples S17 to S21) and post-monsoon from a tributary to the Modi Khola at 3560 m (sample A1). Previous work has shown that the ratio of carbonate to silicate inputs to the TSS Marsyandi catchment decreases during the dry season attributed to deeper groundwater flow paths (Tipper, Bickle, et al., 2006). The tributaries draining the TSS have ⁸⁷Sr/⁸⁶Sr between 0.7145 to 0.7335 and high concentrations of Sr (1000 to 6300 nmol/L) (table 1, fig. 3). The ⁸⁷Sr/⁸⁶Sr ratios are within the range reported for carbonates within the TSS (0.71 to 0.75, e.g., Bickle et al., 2015; Jacobson et al., 2002). Sr/Ca ratios (quoted as mmol/mol ratios) vary from 1.7 to 3.9. δ^88/86Sr ranges from 0.238 to 0.295‰ in the Marsyandi and the one sample from a tributary to the Modhi Khola in the TSS has a δ^88/86Sr of 0.314‰.

Bedloads from tributaries to the Marsyandi and one mainstem Marsyandi sample (BCT10, table 2) have whole bedload ⁸⁷Sr/⁸⁶Sr ratios between 0.712 and 0.720 and δ^88/86Sr values between 0.219‰ and 0.352‰. Acetic acid leaches of TSS bedloads from the Marsyandi, which represent the calcite fraction, have δ^88/86Sr values between 0.260 and 0.318‰. Bickle et al. (2015) report a more extensive set of acetic acid leaches of TSS bedloads and these have ⁸⁷Sr/⁸⁶Sr ratios between 0.711 and 0.7135, Sr contents between 2000 and 4000 mmol/kg, Ca contents between 3000 and 4000 mmol/kg, Sr/Ca ratios between 0.625 and 0.825 (mmol/mol) and Mg/Ca molar ratios between 0.042 to 0.52. Mg/Ca ratios of HCl leaches are similar consistent with observation that dolomite is absent from the Marsyandi TSS catchment.

4.2. The High Himalayan Crystalline Series (HHCS)

Streams draining two units of contrasting lithologies have been sampled in the HHCS. The Dudh Kola and the Indrawati catchments comprise typical HHCS lithologies of high and medium grade gneisses, migmatites and quartzites. Tributaries draining these units have intermediate ⁸⁷Sr/⁸⁶Sr ratios (0.7269 to 0.7445, Kisakürek et al., 2005, fig. 3) at the low end of the range for silicate rocks in the HHCS (0.73 to 0.90; e.g., Ahmad et al., 2000; Jacobson et al., 2002). Concentrations of Sr in streams that drain the HHCS range from 40 to 139 nmol/L in the Dudh Kosi at high altitudes (~2500 to 4000 m), to 118 to 455 nmol/L in Indrawati at lower altitudes (<1000m). Rain and hot-spring corrected Sr/Ca values are also lower in the Dudh Kosi (~ 1.1) than the Indrawati (~2.1). δ^88/86Sr in the Dudh Kosi ranges from 0.320 to 0.449‰ (mean 0.373, n=8). The Indrawati is slightly lower, ranging from 0.274 to 0.390‰ (mean 0.318‰, n=6). Samples from both rivers were taken in both pre- and post-monsoon but the average Sr-isotopic compositions in these different seasons exhibit no systematic differences (table 1). Samples A10 and S6 were collected from the mainstem Indrawati and have δ^88/86Sr values in the same range as the Dudh Kosi, as does sample S7 from a small tributary in a predominantly gneissic unit. Samples A11 and S8 with a lower δ^88/86Sr of 0.274‰ and 0.278 ‰ are from small streams which traverse a carbonate-bearing schist unit (Duvadi et al., 2005). The samples from the Annapurna region (S22 from the Dudh Khola and S24 from the Dana Khola which drain into the Marsyandi and A2 and A3 from small tributaries to the Modi Khola), drain Formation II rocks which are high grade calc-silicate rocks whose assemblages include amphibole, diopside, scapolite and an average of ~ 27 volume % calcite (Becker, 2005). Their ⁸⁷Sr/⁸⁶Sr ratios (0.717 to 0.725, fig. 3) are significantly lower than those of the silicate dominated HHCS but their δ^88/86Sr values (0.347 to 0.427‰) are similar to the other HHCS rivers. In the calc-silicates the Ca-Mg silicate minerals are primarily a product of dolomite breakdown reactions. Thus, the Sr-isotopic compositions of the carbonate and silicate minerals will have been brought to equilibrium during the Himalayan metamorphism.

Figure 3.A), B) and C) δ^88/86Sr values plotted against Sr/Ca, Mg/Ca and ⁸⁷Sr/⁸⁶Sr for water samples (table 1) corrected for cyclic and hot spring inputs as in Bickle et al. (2015). Higher Sr/Ca and Mg/Ca ratios associated with lower δ^88/86Sr values in the carbonate-rich TSS catchments interpreted to result from precipitation of secondary calcite. D) Calcite saturation index, SI, calculated using PHREEQC v3 with the PHREEQC database (sample analyses, pH and temperature given in table 1 and table S1 supplementary information), versus Sr/Ca.

The acetic acid leach of only one sample of HHCS bedload (sample BCT81 from the Indrawati) has been analyzed. This contains very little Sr (50 mmol/kg) with high Sr/Ca and Mg/Ca ratios, a high ⁸⁷Sr/⁸⁶Sr ratio (0.737) and a low δ^88/86Sr value (0.126‰). The very low Sr content would make the leach composition sensitive to addition of components leached from silicate minerals as its relatively high Na/Ca ratio (51 mmol/mol) attests. The high Mg/Ca ratio (0.3) implies that the carbonate leached is 40% (mol fraction) dolomite.

4.3. Lesser Himalayan Series (LHS)

Waters from tributaries of the Bhoti Kosi draining the LHS have very radiogenic ⁸⁷Sr/⁸⁶Sr ratios (0.7947 to 0.8630) similar to the carbonate and silicate rocks from the LHS (e.g., Bickle et al., 2001; Oliver et al., 2003) and intermediate levels of Sr (150 to 334 nmol/L). Sr/Ca ratios of 0.27 to 0.60 are low (table 1, fig. 3). The δ^88/86Sr values of the waters span a wide range from 0.050 to 0.378‰, and there are no detectable differences between samples taken pre- and post-monsoon. The acetic acid leach of LHS bedload sample BCT77 from a small tributary to the Bhote Kosi contains little Sr (107 mmol/kg) and has a high Mg/Ca ratio (0.77) implying that most of the leached carbonate is dolomite. This sample has an ⁸⁷Sr/⁸⁶Sr ratio of 0.751 and a δ^88/86Sr value of 0.345‰, the high δ^88/86Sr value being consistent with exchange with silicate minerals, characteristic of LHS carbonates (e.g., Bickle et al., 2001). The wide range of the δ^88/86Sr values of the LHS samples is intriguing but more data are needed on the bedrock samples to interpret the data.

Figure 4.Histogram of δ^88/86Sr values classified by litho-tectonic unit. Carbonate-bearing units from HHCS (Formation II in the Annapurna region and calc-schist containing units in Indrawati catchment) distinguished. Means and 2 x standard error uncertainties of means are shown for the major litho-tectonic units.

5. DISCUSSION

5.1. Lithological control

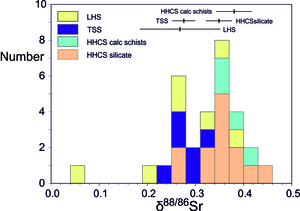
A key control on the water δ^88/86Sr values appears to be lithology with rivers draining carbonate-dominated catchments (e.g., the TSS) exhibiting lower δ^88/86Sr values than those draining silicates (e.g., the HHCS, figs. 3, 4, table 1), as expected from the global compilation of rock δ^88/86Sr values (fig. 1). Thus, rivers draining the silicate-dominated HHCS formation I in the Dudh Kosi catchment tributaries have a mean δ^88/86Sr value of 0.373 ± 0.030‰ (2se, n=8), and in the Indrawati catchment 0.318 ± 0.038‰ (n=6). The carbonate-dominated TSS catchments in the Marsyandi have a mean δ^88/86Sr value of 0.268 ± 0.022‰ (n=5). A small tributary to the Modi Khola in the TSS has a δ^88/86Sr value of 0.314‰. The mean δ^88/86Sr value of the Dudh Kosi and Indrawati silicate catchment tributaries (0.349 ± 0.027‰, 2se n=14) is significantly higher than the mean of the TSS carbonate-dominated tributaries (0.276 ± 0.024‰, n=7) with the probability of the two distributions being indistinguishable ~0.001 (Welch’s t-test).

5.2. Sr-isotope exchange between silicate and carbonate minerals

The δ^88/86Sr analyses of acetic acid leaches of four samples of the Marsyandi bedloads overlap at the 2σ level and have a mean value of 0.270 ± 0.032 ‰ (2σ), a scatter comparable with the estimated external reproducibility of the analyses (table 2). The fifth sample, BCT21, has a higher δ^88/86Sr value (0.318) and higher ⁸⁷Sr/⁸⁶Sr ratio (0.7149) (fig. 5A). This shift in both the radiogenic and stable Sr-isotopic composition of BCT21 carbonate, the sample with the smallest fraction of carbonate Sr (table 2), is consistent with the observation that Himalayan metamorphism has caused Sr-exchange between silicate and carbonate minerals (e.g., Bickle et al., 2001) with the silicates characterised by higher ⁸⁷Sr/⁸⁶Sr and δ^88/86Sr ratios. The much greater abundance of carbonates in the TSS catchment is reflected in their lower ⁸⁷Sr/⁸⁶Sr and δ^88/86Sr ratios than the HHCS samples.

Figure 5.Sr isotopic compositions of TSS Marsyandi bed load samples. Error bars 2σ A) δ^88/86Sr plotted against ⁸⁷Sr/⁸⁶Sr ratios for bedload acetic acid leaches. B) δ^88/86Sr of acetic acid leaches plotted against δ^88/86Sr of whole bed-load analyses. C) ⁸⁷Sr/⁸⁶Sr ratios of acetic acid leaches plotted against ⁸⁷Sr/⁸⁶Sr ratios of whole bed-load analyses. 2σ uncertainties (table 2) smaller than symbols.

Three of the five acetic acid leaches (BCT10, BCT18 & BCT21) have δ^88/86Sr values within error of the whole bed-load values although the ⁸⁷Sr/⁸⁶Sr ratios of the whole bed-load and acetic acid leaches of these samples differ significantly, reflecting the much larger signal-to-precision ratio of the ⁸⁷Sr/⁸⁶Sr system (fig. 5B & C). It should be noted that even if carbonates exchange Sr with silicate minerals, this takes place over length scales of less than a metre (Bickle et al., 2001). Therefore, the bulk carbonate and silicate fractions in bedload derived from lithologically diverse catchments would not necessarily exhibit apparent equilibrium in Sr-isotopic compositions even if equilibrium was attained within individual lithological units.

Two of the bedload samples were collected from the same small stream in 2002 pre- and post-monsoon (BCT23 and ETT34B) and their whole bed-load δ^88/86Sr values are distinct well outside of uncertainty (0.22‰ vs 0.35‰). It is likely that the bedload of the smaller tributaries are not well mixed and reflect individual landslide events (e.g., Niemi et al., 2005). This may also explain why the δ^88/86Sr value of the acetic leach from BCT19 (0.29) is much higher than the whole bed-load sample (0.22 ‰) and the water sample (S18, 0.238 ‰).

The best estimate of the mean carbonate δ^88/86Sr value in the Marsyandi is from the acetic acid leach of sample BCT10 (0.260) which represents an average of the whole Marsyandi TSS catchment. This is higher than the average present-day marine carbonate (0.19 ‰, fig.1) and the flux-weighted mean δ^88/86Sr value of Sr exported from the oceans of 0.21 ± 0.02 (2σ) (Krabbenhöft et al., 2010). This is just within error of the average δ^88/86Sr value of deep ocean carbonate oozes of 0.23 ± 0.02 (2σ) analyzed by Voigt et al. (2015). As discussed above, the carbonate δ^88/86Sr values in the Marsyandi bedload are likely elevated from the original sedimentary (post-diagenetic) composition of the source limestones by exchange with silicate Sr during the Himalayan metamorphism. This is reflected by their ⁸⁷Sr/⁸⁶Sr ratios (0.711 to 0.714) which are well above pristine marine carbonate values (0.707 to 0.709). Elevation of the ⁸⁷Sr/⁸⁶Sr ratio of the carbonate fraction of BCT10 from a likely marine value of ~ 0.708 would require that ~ 20% of its Sr was derived from silicate with a ⁸⁷Sr/⁸⁶Sr ratio of 0.731, that of the silicate residue from leaching (Bickle et al., 2015). If the original silicate had a δ^88/86Sr value of ~ 0.35‰, the mean of silicate catchments sampled here, subtraction of 20% of silicate Sr implies that the pre-Himalayan metamorphism carbonate δ^88/86Sr value would have been 0.23‰.

5.3. Secondary weathering processes: precipitation of calcite

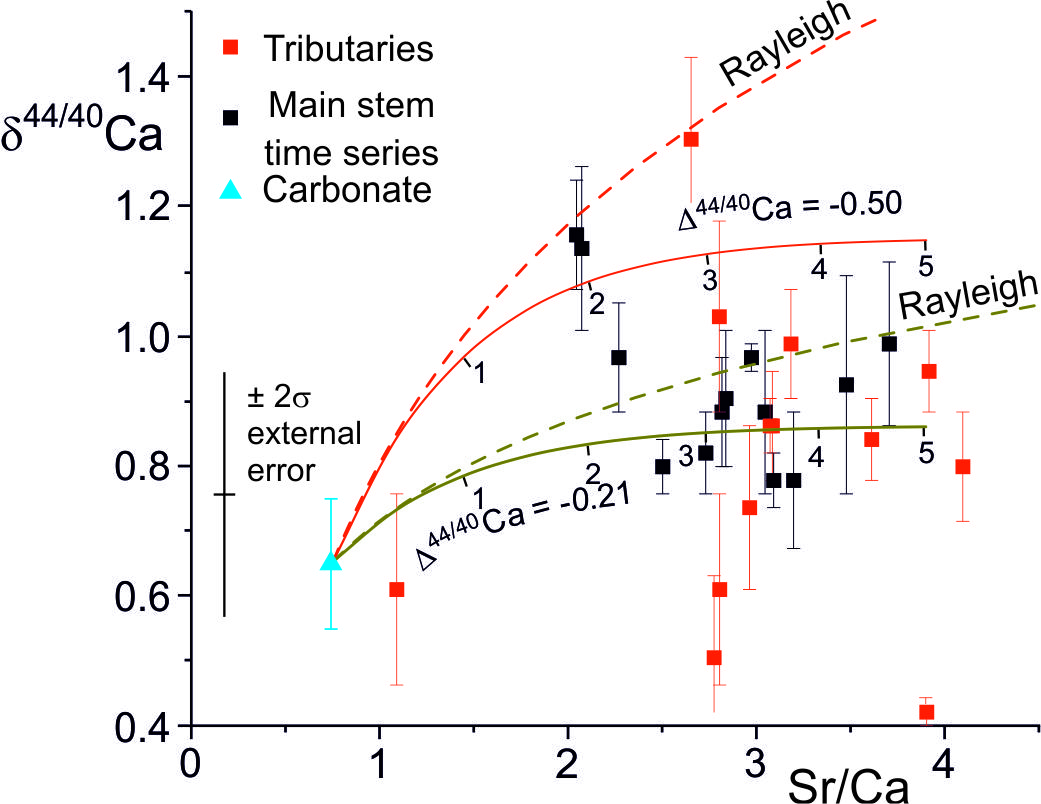
The similarity between the estimates of the δ^88/86Sr values of the carbonate inputs to the Marsyandi waters (0.26‰) and the carbonate source bed-loads (0.27‰) is perhaps surprising given that previous work has argued that between 65 and 80% of the dissolved Ca has been precipitated as secondary calcites (Bickle et al., 2015). The magnitude of stable-Sr-isotopic fractionation between fluid and calcite (~ -0.05 to -0.30 ‰, e.g., Böhm et al., 2012) implies that the fluid δ^88/86Sr values may be fractionated by precipitation of the secondary calcites. We examine models for secondary calcite precipitation and Sr-isotopic fractionation to reconcile this observation and constrain the kinetics of the processes.

The elevation of Sr/Ca and Mg/Ca ratios by precipitation of secondary calcite in Himalayan rivers has previously been modelled by Rayleigh fractionation from a starting solution with Sr/Ca and Mg/Ca ratios of the source carbonate (e.g., Bickle et al., 2015; Galy et al., 1999; Jacobson et al., 2002). In this model the inferred maximum loss of 70 to 80% Ca from the waters implies very high starting Ca concentrations (e.g., Ca ~ 5000 mol/L in the Marsyandi time series samples collected near Chame; Tipper, Galy, et al., 2006). A similar high Ca starting composition was inferred for rivers and springs in the Jura Mountains if their elevated Sr/Ca ratios reflected Rayleigh fractionation (Calmels, 2007). Such high Ca concentrations, charge balanced by HCO₃^- are implausible unless the carbonate system in the river is far from equilibrium with the atmosphere. They are also significantly higher than the maximum concentrations of ~ 3500 μmol/L seen in a global dataset of carbonate-draining river compositions compiled by Gaillardet et al. (2019), higher than any tributaries and cold springs in the Marsyandi catchment (maximum 1825 μmol/L Ca) and only surpassed by hot springs. However, the latter have significant inputs of CO₂ derived from metamorphic decarbonation reactions (Becker et al., 2008), are confined to the Marsyandi mainstem valley bottom and make negligible contributions to the tributaries in which the δ^88/86Sr ratios reported here were measured (Evans et al., 2004).

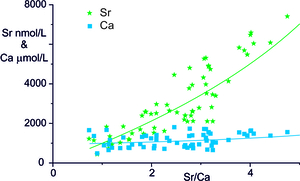
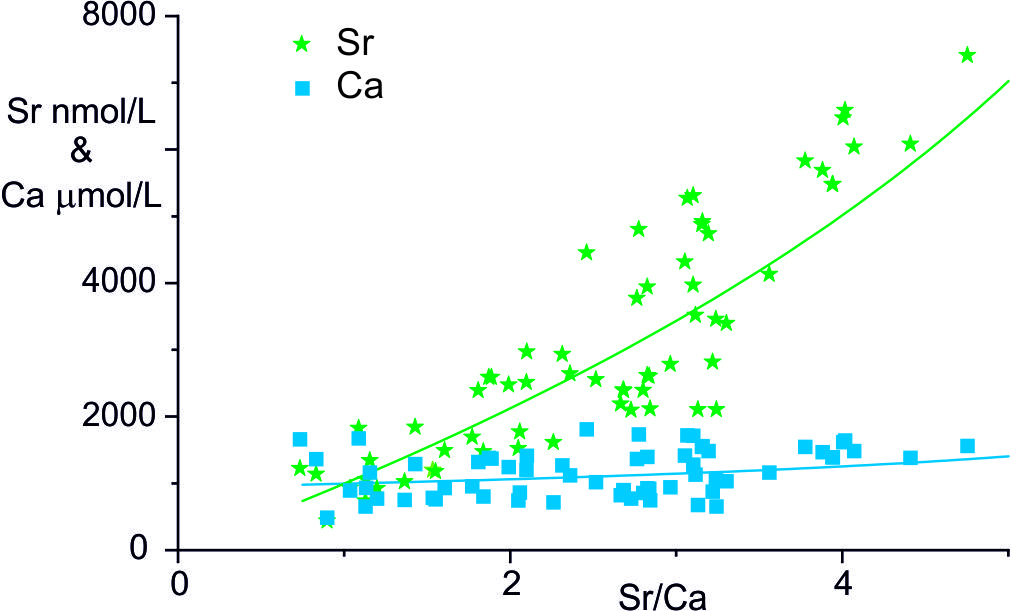
An alternative mechanism to explain the high Sr/Ca and Mg/Ca ratios in river waters suggested by Calmels (2007) is that the calcite re-crystallises by a solution-exchange process so that the water Ca concentrations may be maintained near a constant concentration. Such a process is used to explain the diagenetic alteration of seafloor sediments where the biogenic high-Mg calcites are unstable with respect to low-Mg calcite and the recrystallisation drives Sr and Mg return fluxes to the ocean (Gieskes et al., 1975; Richter & DePaolo, 1987). The key observation that Gieskes and Kastner (1975) made to justify the assumption of recrystallisation of the original high Sr-carbonate to a low Sr-carbonate was that the fluid showed a much larger increase in Sr than Ca concentrations. The waters in the Marsyandi show comparable trends with a negligible change in Ca concentration with Sr/Ca ratio whereas Sr concentration increases by a factor of ~ 9 (fig. 6). These trends do not represent mixing with inputs from silicate weathering as these are small based on analyses of silicate fractions of Marsyandi bedloads (Bickle et al., 2015).

We therefore evaluate a solution-repreciptation model to explain the elevated Sr/Ca in Himalayan waters and calculate how Sr and Ca concentrations and stable Sr and Ca isotopic ratios might be expected to vary with Sr/Ca ratios as a function of re-precipitation rate.

Figure 6.Variation of Ca and Sr against Ca/Sr ratio for the times series samples collected over two years at Chame in the mainstem Marsyandi close to where it leaves the TSS catchment (Tipper, Bickle et al., 2006). Lines denote the best fit for the evolution of Ca and Sr concentrations (eqs S18 and S23 in supplementary information) for a dissolution-reprecipitation model which gives ε= -0.04 ± 0.05 (1σ), where ε is the fractional difference in the rate of precipitation of secondary calcite to dissolution of primary calcite. Calculated given $K_{D}^{Sr/Ca}$ = 0.05, ${Sr}_{F}^{0}$ = 735 nmol/L and ${Ca}_{F}^{0}$ = 980 μmol/L. Ca and Sr are corrected by subtracting silicate inputs calculated using the Na/Ca and Sr/Ca ratios of the leached BCT10 bedload (Bickle et al., 2015).

6. MODELS FOR PRECIPITATION OF SECONDARY CALCITE

6.1. Fractionation factors for water-calcite δ^88/86Sr values

The fractionation factors between water and calcite stable Sr- and Ca-isotopic ratios (∆^88/86Sr, ∆^44/40Ca) are inversely related to the Sr/Ca partition coefficient ($K_{D}^{Sr/Ca}$) (fig. 7A), defined as,

$$K_{D}^{Sr/Ca} = \frac{\left. \ Sr/Ca \right|_{calcite}}{\left. \ Sr/Ca \right|_{water}} \tag{1}$$

The Sr/Ca partition coefficient and isotopic fractionation factors are functions of fluid chemistry and temperature and precipitation rate (fig. 7B). However, their covariation is, within the precision of the data, only dependent on precipitation rate (AlKhatib & Eisenhauer, 2017; Böhm et al., 2012; DePaolo, 2011; Gabitov et al., 2014; Z. Zhang & Wang, 2024). Models of the processes which control the Sr- and Ca-isotopic and Sr/Ca partition coefficient infer kinetic control by a surface reaction process although they differ on details of the process (e.g., DePaolo, 2011; Mills et al., 2021; Z. Zhang & Wang, 2024). Data from laboratory experiments and natural samples for water compositions with high Ca²⁺$:{CO}_{3}^{2 -}$ ratios is consistent with the ∆^88/86Sr and ∆^44/40Ca isotopic fractionations being close to zero at equilibrium, that is at low reaction rates, and tending to a limit (∆^88/86Sr ~ -0.4‰, ∆^44/40Ca ~ -2‰) at rapid reaction rates (Z. Zhang & Wang, 2024). Zhang and DePaulo (2021) infer that the equilibrium value of the Sr/Ca partition coefficient is ~ 0.025 from slowly precipitated marine calcites and Zhang and Wang (2024) estimate that $K_{D}^{Sr/Ca}$ = 0.24 at the kinetic limit. This allows the Sr and Ca isotope and elemental partitioning coefficients to be parameterised with relatively simple and self-consistent expressions against precipitation rate (Z. Zhang & Wang, 2024). The covariation of stable Sr- and Ca-isotopic ratios with Sr/Ca ratios can therefore be used to put further constraints on the rate and mechanisms of secondary calcite precipitation.

Figure 7.A) Correlation between calcite-water stable Sr isotopic fractionation factor and calcite-water Sr/Ca partition coefficient (1. AlKhatib & Eisenhauer, 2017; 2. Böhm et al., 2012; 4. Fruchter et al., 2017; 3. Shalev et al., 2017). Line and 1σ error bounds least squares fit taking into account quoted errors on both δ^88/86Sr and $K_{D}^{\frac{Sr}{Ca}}$ after Kent et al. (1990). B) Compilation of experimental determinations of calcite-water Sr/Ca partition coefficient compiled by Gabitov et al. (2014).

6.2. Modeling calcite solution and re-precipitation

6.2.1. Introduction

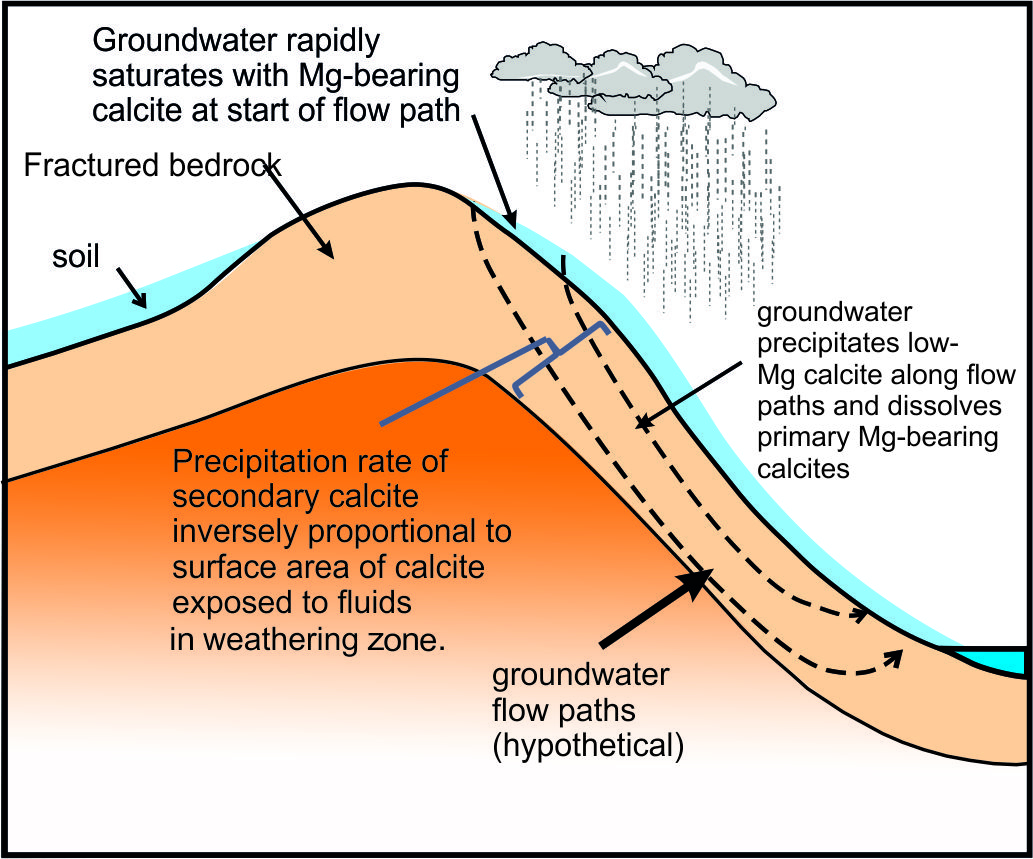
We model the isotopic and elemental fractionations caused by the calcite solution and re-precipitation process by reactive transport along a one-dimensional flow path through a porous medium (cf. Fontorbe et al., 2013; Maher, 2010). We consider the evolution of a fluid flowing through a carbonate rock matrix in which the reactions with calcite dominate the water chemistry. Further, since the kinetics of calcite solution are rapid, we envisage that the fluid approaches calcite saturation near to the start of the flow path. In rapidly eroding Himalayan catchments where solution reactions are incomplete it may be assumed that the composition of the rock, reaction rates and isotopic fractionation factors remain constant with time and that the time-varying term in the differential equation is small (see discussion of the quasi-steady state assumption in Lichtner (1988) and discussion of the results of our modeling below). Therefore, the concentration of a component in the fluid (e.g., Ca_F) at any given distance, x, is assumed constant with time.

6.2.2. Mathematical Models

The equations describing the evolution of Ca, Sr and their isotopic ratios, making the stationary-state assumption (Lichtner, 1988), may be written as a function of the precipitation to dissolution rate (terms are defined in table S4 in supplementary information). The mass balance of Ca (mol m^-3) is given by

$$\omega_{0}\phi\frac{{\partial Ca}_{F}}{\partial x} = R_{Ca} - R_{Ca}(1 + \epsilon) = - R_{Ca}\ \epsilon \tag{2}$$

where R_Ca is the rate Ca is supplied by mineral dissolution (mol Ca m^-3 s^-1 ) and 1+ ε describes the rate of precipitation of secondary calcite relative to the rate of supply by mineral dissolution. When ε= 0 re-precipitation balances dissolution, when ε = -1 re-precipitation is zero and when ε → ∞ the system tends to Rayleigh fractionation with dissolution negligible compared to precipitation.

Making the approximation that the range of isotopic compositions is small, the variation in Ca-isotopic values with reactive transport may then be described by

$$\begin{align} &\frac{\partial\left( \delta^{\frac{44}{40}}Ca.{Ca}_{F} \right)}{\partial x} = \\ &\quad R_{Ca}\ {\delta^{\frac{44}{40}}Ca}_{CC} \\ &\qquad - (1 + \epsilon)\ R_{Ca}.\left( \delta^{\frac{44}{40}}Ca + \Delta^{\frac{44}{40}}Ca \right) \end{align} \tag{3}$$

where Ca_F is given by the solution to equation (2).

The differential equation for the variation of Sr concentration in the fluid (Sr_F, nmol m^-3) with distance is

$$\begin{align} \omega_{0}\phi\frac{{\partial Sr}_{F}}{\partial x} &= \left. \ \frac{Sr}{Ca} \right|_{CC}\ R_{Ca} \\ &\quad - \frac{{Sr}_{F}}{{Ca}_{F}}{\ K}_{D}^{\frac{Sr}{Ca}}\ R_{Ca}\ (1 + \epsilon) \end{align} \tag{4}$$

where $K_{D}^{Sr/Ca}$ is the calcite-fluid Sr/Ca partition coefficient and $\left. \ \frac{Sr}{Ca} \right|_{CC}$the source calcite Sr/Ca ratio. The approximate differential equation describing the mass-balance of Sr-isotopic compositions is

$$\begin{align} &\frac{\partial\left( \delta^{88/86}{Sr}_{F}.{Sr}_{F} \right)}{\partial x} = \\ &\quad R_{Ca}\ \delta^{88/86}{Sr}_{CC}\ \left. \ \frac{Sr}{Ca} \right|_{cc} \\ &\qquad - R_{Ca}\ K_{D}^{Sr/Ca}\ \left. \ \frac{Sr}{Ca} \right|_{cc}\ \left( \delta^{88/86}{Sr}_{F} + \Delta^{88/86}Sr \right) \end{align} \tag{5}$$

where Ca_F and Sr_F are given by the solutions to equations (2) and (4).

The following are convenient transformations to dimensionless variables,

$$x = h\ {x}^{\prime}$$

$$Sr = {Sr}_{F}^{\prime}\ {Sr}_{F}^{0}$$

$$Ca = {Ca}_{F}^{\prime}\ {Ca}_{F}^{0} \tag{6}$$

where h is a length scale (here flow path length) and ${Sr}_{F}^{0}$ and ${Ca}_{F}^{0}$ are the initial fluid concentrations. For given starting compositions these transformations allow the differential equations to be rewritten in terms of one variable, a Damköhler number, which defined as

$$N_{D} = \frac{R_{Ca}\ h}{{Ca}_{F}^{0}\ \omega_{0}\ \phi}\tag{7}$$

An alternative Damköhler number, normalised to the initial concentrations of calcite Ca in the bulk rock ($N_{D}^{rock}$), maybe used to describe the extent of rock re-crystallisation and is related to N_D by

$$N_{D}^{rock} = \frac{{Ca}_{F}^{0}}{{Ca}_{CC}}\ N_{D} \tag{8}$$

The solutions to equations (2) to (5) are given in the supplementary section S5, equations (S12) to (S21).

Figure 8.The evolution of δ^88/86Sr values against Sr/Ca ratios from water with initial Sr/Ca = 0.75 and δ^88/86Sr = 0.254‰ for values of ε = -0.5, 0 and 0.5 as well as by Rayleigh fractionation for values of $K_{D}^{\frac{Sr}{Ca}}$ and Δ^88/86Sr shown. Damköhler numbers shown on curves. Calculated from equation (S17) and with equation (5) solved by a numerical routine. Curves for ε= -0.5 and 0 extend to their equilibrium Sr/Ca and δ^88/86Sr values. For the ε=0.5 curves Ca goes to zero at N_D = 2.

6.2.3. Implications of the reactive transport model

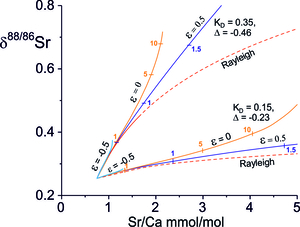
The solutions for the covariation of δ^88/86Sr values and Sr/Ca ratios for ε = -0.5, 0, +0.5 and ∞ (Rayleigh fractionation) for Sr-isotope and Sr/Ca fractionation factors appropriate to two precipitation rates from the correlation in figure 7A are shown in figure 8. This illustrates the major control on trajectories in δ^88/86Sr-Sr/Ca ratio space is precipitation rate which determines the fractionation factors. Paths in which precipitation is less than dissolution (ε<0) are limited and go rapidly to steady state because the fluid composition is dominated by the dissolving calcite. Solutions with precipitation greater than dissolution (ε>0) approach Rayleigh fractionation as ε becomes large. Natural systems will deviate from these idealized trends as fluids either become saturated in primary calcite (ε<0) or depleted (ε>0) and where the extent of reaction will be controlled by the extent of initial under- or over-saturation of calcite. In carbonate flow paths where the solution and re-precipitation of calcite is driven by the small difference in free energy between the primary Mg-calcite in the rock and the product low Mg-calcite it seems likely that re-precipitation will balance dissolution such that the Ca content of the fluid remains nearly constant. In such a system solution and re-precipitation rates will decrease slowly as fluid Mg/Ca ratios increase.

Figure 9.The evolution of δ^88/86Sr values against Sr/Ca ratios from water with initial Sr/Ca = 0.75 and initial Δ^88/86Sr = 0.254‰ calculated from equations (S18) & (S20) for constant Ca in fluid (ε=0) for values of $K_{D}^{\frac{Sr}{Ca}}$ and δ^88/86Sr shown (black curves which extend to equilibrium values). Damköhler number shown as dotted black contours (note that Damköhler number scales with distance along the flow path). Rayleigh fractionation curves (dashed, red) evolve to lower δ^88/86Sr values for the equivalent Sr/Ca ratio. Data points are TSS samples from the Marsyandi and Modi Khola with 2σ internal error bars shown where larger than the symbol (table 1) and the lower ⁸⁷Sr/⁸⁶Sr acetic acid leaches of TSS bedloads (table 2).

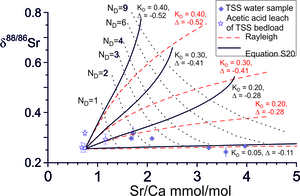
The evolution of δ^88/86Sr values against Sr/Ca ratios for balanced solution and re-precipitation (ε=0) is illustrated in figure 9 as a function of the Damköhler number for a range of $K_{D}^{\frac{Sr}{Ca}}$ and Δ^88/86Sr fractionation factors which co-vary as the experimentally determined precipitation-rate dependent correlation (fig. 7A). The solutions depend on the starting composition of the water, taken as the lowest bedload carbonate leach of TSS bedload, on the Sr/Ca partition coefficient and on the Damköhler number. The latter is proportional to reaction rate and flow path length and inversely proportional to the fluid flux. At low precipitation rates both Δ^88/86Sr and $K_{D}^{\frac{Sr}{Ca}}$ are small and the Sr content of the fluid is dominated by the addition of Sr from the rock. The result is that there is little change in δ^88/86Sr values, but the fluid Sr/Ca ratios increase rapidly because the secondary calcite has low Sr/Ca ratios relative to the source carbonate. At higher precipitation rates both ∆^88/86Sr and $K_{D}^{\frac{Sr}{Ca}}$ are larger and the fluid δ^88/86Sr values increase more rapidly with Damköhler number (distance), but Sr/Ca ratios increase more slowly. With Rayleigh fractionation water compositions evolve to higher Sr/Ca ratios at equivalent δ^88/86Sr values because Ca is more rapidly depleted in the fluid.

Figure 10.δ^44/40Ca for Marsyandi TSS tributary samples and mainstem time series water samples plotted against Sr/Ca ratio (Tipper, Bickle, et al., 2006; Tipper et al., 2008; Tipper, Galy, et al., 2006, δ^44/40Ca taken as equal to 2.1* δ^44/42Ca). Solid curves show reactive transport trajectories calculated with balanced dissolution-re-precipitation (ε=0) with a starting composition δ^44/40Ca = 0.65‰ (mean of three carbonate samples, Tipper, Bickle et al., 2006), Sr/Ca=0.75 and with Damköhler numbers marked. Calculated for calcite-water ∆^44/40Ca isotopic fractionations of -0.21 and -0.50‰ and $K_{D}^{\frac{Sr}{Ca}}$= 0.05. Note that if $K_{D}^{\frac{Sr}{Ca}}$ is increased the shape of the curves only changes slightly but the locii of the Damköhler numbers shift towards the starting point. Dashed curves show δ^44/40Ca versus Sr/Ca ratio for Rayleigh fractionation with the same Ca-isotopic and Sr/Ca fractionation factors. Error bars 2σ internal errors on water samples and 2xstandard error on mean of three carbonate samples.

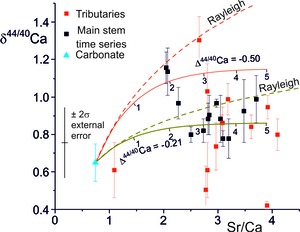
The Ca-isotopic compositions of the waters are also a function of the Ca-isotope fractionation factor, itself a function of the precipitation rate and the Damköhler number (fig. 10). However, δ^44/40Ca values of the waters vary more rapidly with calcite solution-reprecipitation than δ^88/86Sr values, especially at lower precipitation rates where $K_{D}^{\frac{Sr}{Ca}}$ is low. This is because fluid Sr isotopic compositions are buffered by the high ratio of Sr derived from mineral dissolution to that lost to secondary calcite, whereas at ε = 0, equal amounts of Ca are added to and lost from the fluid.

6.3. Interpretation of the Himalayan data

The modeling of stable Sr- and Ca-isotope analyses in conjunction with the water chemistry is used to elucidate the mechanism, magnitude and rates of formation of secondary calcites in the carbonate-dominated Marsyandi TSS catchment. The rates are compared to carbonate re-crystallisation rates inferred from catchment Ca fluxes and water-rock interactions in the Marsyandi catchment. The modeling enables comparison of the carbonate reaction rates with silicate reaction rates inferred from a similar analysis of Li isotopic compositions (Bohlin & Bickle, 2019).

6.3.1. Sr- and Ca-isotopic fractionations and precipitation rates

The TSS water samples from the Marsyandi and the Modi Khola have low Na/Ca ratios, but high Sr/Ca and Mg/Ca ratios (fig. 3) which is characteristic of carbonate-dominated catchments in which Sr/Ca and Mg/Ca ratios have been elevated by precipitation of secondary calcite. Waters in these catchments are also calcite-saturated or supersaturated (fig. 3D). The δ^88/86Sr values show limited variation despite the high Sr/Ca ratios which have been elevated from the source limestone values by as much as a factor of 4 and plot in the region characterised with calcite precipitation rates ≤ 10^-2 nm s^-1 ($K_{D}^{\frac{Sr}{Ca}}$ ≤ 0.05, Δ^88/86Sr ≥ -0.11‰, fig. 9). The Mg/Ca ratios exhibit similar elevations above the source limestone Mg/Ca ratios. However, their δ²⁶Mg compositions (Tipper, Galy, et al., 2006) are elevated by ~ 1‰ above bedload carbonate, consistent with the estimate of Bickle et al. (2015) that between 30 and 60% of the Mg in the waters is silicate-derived. This precludes the use of the correlation of Mg-isotope fraction factors with precipitation rates (Mavromatis et al., 2013), as such shifts would swamp the ~0.1‰ Mg-isotopic fractionation factors for calcite re-precipitation.

The δ^88/86Sr-Sr/Ca trajectories for balanced solution and re-precipitation and Rayleigh fractionation are indistinguishable at these low fractionation factors. However, as discussed in section 5.3, only a near-balanced solution-reprecipitation process is plausible as Sr concentrations increase as Ca concentrations remain approximately constant (fig. 6); also, because the low free energy difference between the Mg-calcite being dissolved and the precipitate calcite requires that the process operates with near-balanced solution and re-precipitation as discussed above. The significant addition of Mg from silicate to the waters complicates estimating Damköhler numbers from the Mg data as sites where silicate weathering products are added to the flow paths are not known. Presuming that Damköhler numbers appropriate to the Sr reactive transport apply to Mg then the secondary calcite precipitated along the flow path would have Mg/Ca ratios between ~ 0.0005 and 0.003 for the maximum likely Mg/Ca partition coefficient 0.01 (Mavromatis et al., 2013) and initial water Mg/Ca ratios of 0.046. Since the primary calcite has a Mg/Ca ratio of 0.046 (± 0.0027, 2se n=7), the mean of acetic acid leaches of bedload (Bickle et al., 2015), minimal changes in the solution-reprecipitation rate due to the increase in Mg/Ca ratios in the waters would be expected along the flow path

The δ^44/40Ca values of the water samples analyzed by Tipper, Galy et al. (2006) (mean δ^44/40Ca = 0.87 ± 0.04 ‰, 2se, n=20) are distinct from leaches of bedrock and bedload carbonate compositions (mean δ^44/40Ca = 0.65 ± 0.17 ‰, 2se, n=3) (fig. 10). As for Sr, Ca concentrations and isotopic compositions would be little changed by the addition of Ca from silicates.

The correlation between stable Sr-isotope fractionation factors, $K_{D}^{\frac{Sr}{Ca}}$ and precipitation rates (fig. 7) implies that precipitation rates in the TSS catchments were less than ~ 10^-2 nm/s given that Δ^88/86Sr is equal to or less than ~ 0.1 ‰. The Ca-isotope fractionation (∆^44/42Ca = -0.21 ± 0.17, 2se) implies precipitation rates between 4.6x10^-4 nm s^-1 and 5.2x10^-3 nm s^-1 (2σ uncertainty on observed ∆^44/42Ca) using the parameterisation of the experimental data compiled by Zhang and Wang (2024). However the additional uncertainty in the functional form of the relationship between Ca-isotope fractionation and precipitation rate (e.g., DePaolo, 2011; Mills et al., 2021; Z. Zhang & Wang, 2024) is rather larger than this and a realistic assessment is that the Ca-isotope data implies precipitation rates of less than ~ 5x10^-3 nm s^-1.

6.3.2. Calcite re-crystallisation rates compared to field constraints

It is of interest to compare the estimated precipitation rates with calculations of the total calcite solution-precipitation rates in the catchment based on the rate of Ca exchange between fluid and minerals given by the modeling, the total flux of Ca through the catchment and the surface area of calcite crystals in contact with the fluid.

The precipitation rate of secondary calcite in the catchment may be constrained by the Damköhler number. The mean Sr/Ca of the Marsyandi time series samples collected near Chame of ~ 2.75 and their small range of δ^88/86Sr values is consistent with an average Damköhler number of ~ 3 (range: 1.6 to 4, fig. 9), comparable with that indicated by the Ca-isotope data (fig. 10). The rate of Ca solution between water and rock along a flow path length h (m) is R_Ca h (mol Ca s^-1 m^-2). The Damköhler number (eq 5) is the ratio of the calcite solution rate along the flow path to the dissolved Ca flux. A Damköhler number of 3 therefore implies that 3 times as much Ca is dissolved, and 3 (1+ε) reprecipitated, as the dissolved Ca flux. Assuming ε = 0, the mass of calcite dissolved and re-precipitated per year is given by the water flux out of the Marsyandi TSS catchment (6.2x10⁸ m³/yr, Gabet et al., 2008) times the Ca concentration of the water (~800 μmol/L, Bickle et al., 2015) times 3, that is 1.5x10⁹ mol/yr. The precipitation rate of the secondary calcite is then given by this precipitation rate divided by the surface area of the calcite in contact with the fluid in the catchment.

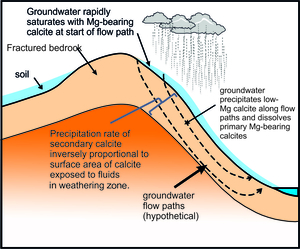
The calcite surface area is a function of the thickness of the weathering zone, and the surface area of exposed calcite within the weathering zone (fig. 11). We assume, as a limiting case, that all the calcite in the top 1 m of the bedrock, in the catchment area of 812 km², is exposed to calcite re-precipitation, that the mean fraction of calcite in the bedrock is 0.34 (fraction of calcite in the bedload sample BCT10, Bickle et al., 2015) and the mean surface area of the calcite is 0.5 m²/g (Heling, 1968). If so, the calcite has a surface area of 4x10¹⁴ m² in the catchment. This implies a growth rate of ~5x10^-9 nm/s, much less than the maximum rates of ~ 5x10^-3 nm/s inferred from the calcite-water ∆^44/42Ca fractionation with the Zhang and Wang (2024) parameterisation and also the ~10^-2 nm/s limiting value at which δ^88/86Sr fractionations in the solution and re-precipitation flow model appear to be sensitive to precipitation rate (fig. 7). The fraction of calcite surface area exposed to fluids in the top metre would need to be less than ~5x10^-5 of the total calcite surface area for the re-precipitation rate to reach 10^-4 nm/s. It is probable that groundwater circulates much deeper than 1 metre and, if so, the fraction of the area of calcite exposed to the groundwater would need to be proportionally less for re-precipitation rates to reach the critical rate of 10^-3 nm/s. It seems very unlikely that re-precipitation rates reach values as high as 10^-3 nm/s, unless flow takes place along widely spaced cracks.

The fraction of the calcite exported in the Marsyandi TSS catchment which is re-precipitated as low Sr- and Mg-calcite, may be calculated from the detrital flux of calcite of ~ 8x10⁹ mol/yr (inferred from a total detrital flux of 2.2x10⁹ kg/yr, Gabet et al., 2008, containing ~34 weight % carbonate) and the solution-reprecipitation rate of 1.5x10⁹ mol Ca yr^-1. This fraction, at ~ 20%, is surprisingly high but addition of the re-precipitated calcite would make a negligible difference to its bulk δ^88/86Sr values as the inferred isotopic fractionation factor is small. Integrating the precipitated calcite composition over the flow path length, the re-precipitated calcite would have a mean δ^88/86Sr ~ 0.10 ‰ less than the Mg-calcite and a mean Sr/Ca ratio of the re-precipitated calcite of ~ 0.1. Addition of this calcite would decrease the bulk δ^88/86Sr of the detrital calcite by ~ 0.02 ‰ and its Sr/Ca ratio from 0.75 to 0.62 but these differences will be undetectable given the precision of the Sr-isotopic measurements and the heterogeneity of the bedload carbonate compositions (table 2 and data in Bickle et al., 2015). The thickness of the re-precipitated rims depends on the mean grain size. If the estimated carbonate surface area of 0.5 m²/g was on uniform sized spherical grains, these would have a diameter of 4 μm, much less than the observed grains in the bedload, and the re-precipitated rim thickness would be ~ 0.15 μm, too thin to be easy to detect.

Figure 11.Schematic figure illustrating model for calcite recrystallisation. Rain water rapidly saturates with Mg-bearing calcites in the limestones at the start of the flow path. As the water flows along groundwater flow paths low-Mg calcite is precipitated replacing the higher Mg-calcite in the weathering zone driven by the small difference in thermodynamic stability between Mg-bearing biogenic limestone and re-precipitated low-Mg calcite. Note ground water flows are likely more complex than shown. Also thickness of soil (thin to absent), weathering zone, (possibly metres to 10’s metres in fractured rock), and height above valley floor (~ 2000 m in the Marsyandi) are not to scale.

6.3.3. Comparison with silicate dissolution rates from Li-isotopic compositions

It is of interest to compare the weathering kinetics inferred from Damköhler numbers derived from δ^88/86Sr values with those inferred from Li-isotopic ratios since the latter reflect silicate weathering with only a minor contribution from carbonates (Kisakürek et al., 2005). The water-normalised Damköhler numbers implied by the Marsyandi δ^88/86Sr values and Sr/Ca ratios (fig. 8) range between ~2 and 6 which translate to rock-normalised Damköhler numbers between 2x10^-4 and 6x10^-4, given the average tributary water Ca concentration (~ 1 mmol/L) and the average bedload calcite Ca concentration of 4.2 mol/kg (Bickle et al., 2015). Rock-normalised Damköhler numbers for Li dissolution in the Marsyandi TSS waters are between 3x10^-5 to 3x10^-4 (Bohlin & Bickle, 2019, fig. F1). The overlap in these estimates might seem surprising given that carbonate dissolution rates are generally at least an order-of-magnitude faster than silicate dissolution rates (e.g., Drever, 1997). However, the covariation of δ^88/86Sr values and Sr/Ca ratios constrains the coupled solution-re-precipitation rate of Mg-calcites to low Mg-calcites from fluids which are presumably only slightly under-saturated with respect to Mg-calcite. These rates will be much slower than the initial dissolution by the original under-saturated rain or ground water compositions.

6.3.4. Implications for quantifying cation inputs from silicate and carbonate minerals

A key question is how the balanced solution-reprecipitation model impacts calculation of the relative proportions of silicate and carbonate inputs to the waters. The Rayleigh fractionation model assumes that the chemical weathering takes place prior to precipitation of secondary calcites as the CO₂ over-saturated waters degas and warm (e.g., Jacobson et al., 2002). If the precipitation of secondary calcite takes place along ground water flow paths, then the relative locations of the silicate and carbonate inputs and calcite solution-reprecipitation reactions will impact the resultant river chemistries. The chemical weathering processes will be governed by how the groundwater flow paths sample the different rock types in the catchment which will be controlled by the range of rock types, their geometries and physical properties. In steep rapidly eroding Himalayan catchments, groundwater flow will be through thin soils, regolith, moraines and variably fractured bedrock. River waters will represent mixtures from groundwater flow paths which may sample different combinations of carbonate rocks, silicate rocks, calc-silicate rocks, alternating carbonate and silicate rocks and variably weathered mixed regolith and moraines.

To illustrate the potential impact of balanced solution-reprecipitation on the calculation of the relative inputs of silicate and carbonate cations we explore a simple end-member model. In this the silicate-derived and carbonate-derived waters mix after passing through separate groundwater flow paths in silicate or carbonate rocks. The mass-balance equations may be written (cf. Bickle et al., 2015, equations 5 and 6)

$$X_{wat}^{i} = \left( {E^{i}F}_{crb.}X_{crb}^{i} + F_{sil\ }X_{sil}^{i} \right) \tag{9}$$

and for ⁸⁷Sr/⁸⁶Sr

$${\phantom{.}}^{87}X$$

$$\small{ \begin{align} &{{\phantom{.}}^{87}{Sr/^{86}{Sr}}}_{wat} \\ &= \frac{\left({{\phantom{.}}^{87}{Sr/^{86}{Sr}}}_{crb\ }{F_{crb}}_{Sr\ }E^{Sr}\ X_{crb}^{Sr} + \ \ {{\phantom{.}}^{87}{Sr/^{86}{Sr}}}_{sil\ }{F_{sil}X}_{sil}^{Sr} \right)}{\left( E_{Sr\ }{F_{crb\ }X}_{crb}^{Sr} + \ F_{sil}X_{sil}^{Sr} \right)} \end{align} \tag{10} }$$

where $X_{wat}^{i}$ is the concentration of cation ‘i’ in the water (mmol/L), F_crb and F_sil the weight of the carbonate and silicate components (kg/L) added to the water by weathering prior to solution-reprecipitation in the carbonate groundwater flow path, $X_{j}^{i}$ the concentration (mmol/kg) of cation ‘i’ in input phase ‘j’ (carbonate or silicate) and Eⁱ is the amount cation 'i’ is enriched by the solution-reprecipitation reactions. Eⁱ equals 1 for Ca, Na and K since Na and K concentrations are not changed by precipitation of secondary carbonates and we model balanced solution-reprecipitation for Ca. The enrichments of Sr and Mg are functions of their respective partition coefficients and the Damköhler number (N_D) as given by equation (7). The variation of Mg calcite-water partition coefficient with precipitation rate is not well constrained with Gabitov et al. (2014) and Mavromatis et al. (2013) observing opposite relationships possibly arising from differences in fluid chemistry. However, $K_{D}^{Mg/Ca}$ in their experiments is constrained to lie between ~ 0.01 and 0.035 and the maximum difference between E^Mg and E^Sr is ~ +12% (at N_D = 5 and with $K_{D}^{Mg/Ca}$= 0.01 and $K_{D}^{Sr/Ca}$= 0.05). To allow for this difference the enrichment fact for Mg (E^Mg) has been parameterized as

$$\ E^{Mg} = \ - 0.0040 + 0.9922\ E^{Sr}\ + \ 0.0127\ {E^{Sr}}^{2}\tag{11}$$

Equations (9) and (10) have then been solved for F_crb,, F_sil, $X_{j}^{i}$, N_D and E^Sr given water Sr, Ca, Mg and ⁸⁷Sr/⁸⁶Sr compositions for the Marsyandi time-series suite of samples and the silicate and carbonate compositions of the bed-load sample BCT10 (table 3). These solutions may be compared with solutions assuming calcite precipitation by Rayleigh fractionation of Bickle et al. (2015, table 2). The fractions of Sr and Mg derived from carbonate in the solution-reprecipitation model are close to those calculated from Rayleigh fractionation because in both models carbonate Sr and Mg are increased to match the observed Sr/Ca ratios and little Sr and Mg are lost to secondary calcite. However, the fraction of silicate-derived Ca delivered to the river calculated for the solution-reprecipitation process is a factor of ~ 3 higher (4.2% versus 1.3%) than calculated by Rayleigh fractionation. This difference arises because with Rayleigh fractionation the initial high Ca (both silicate and carbonate-derived) is lost to secondary calcite. With solution-reprecipitation restricted to groundwater flow paths in carbonate, silicate-derived Ca is not lost. Clearly the nature of the groundwater flow paths which control how waters interact with silicate and carbonate rocks are important controls on chemical weathering outputs and will impact the calculation of the relative inputs from silicate and carbonate sources.

The results are consistent with a major conclusion of Jacobson et al. (2002) that secondary calcite precipitation elevates Sr/Ca and Mg/Ca and precludes direct use of these ratios to estimate silicate and carbonate inputs. The modeling of balanced solution-reprecipitation in the system Sr-Ca-Mg-⁸⁷Sr/⁸⁶Sr implies water Na and K concentrations much higher than those measured (table 3) as was observed with the Rayleigh fraction model of Bickle et al. (2015). Modeling including Na, e.g., in the system Na-Sr-Ca-Mg-⁸⁷Sr/⁸⁶Sr, returns solutions with a much poorer fit (average χ² ~ 119 for the time series samples versus 0.6 for Sr-Ca-Mg-⁸⁷Sr/⁸⁶Sr system). A possible reason is that Na and K in rocks, from this mainly low metamorphic grade catchment, are hosted in white micas which weather slowly compared to the minerals hosting Sr, Ca and Mg. The result is that the silicate fractions of the bed load have much higher ratios of Na to Ca, Mg and Sr than the cations released to solution. This illustrates a significant uncertainty in calculating the relative inputs of silicate and carbonate minerals which is the choice of appropriate element ratios of the silicate inputs. The goodness of fit, ie. low χ², is a necessary indication that waters and chosen input end-member ratios lie in the appropriate hyperplane defined by the input compositions but does not require that the input phase compositions lie in their correct positions (cf. Sohn, 2013). This is a fundamental limit to the ‘inversion’ method for calculating carbonate and silicate inputs (e.g., Gaillardet et al., 1999; Moon et al., 2014; Négrel et al., 1993) since the inversion will yield results in which the input phase compositions lie in the mixing hyperplane defined by the water compositions but cannot determine their locations within the hyperplane.

7. Conclusions

This study shows that the δ^88/86Sr isotopic values of carbonate in Himalayan rocks are elevated by exchange with silicate minerals as observed for ⁸⁷Sr/⁸⁶Sr ratios. Carbonate-dominated catchments (e.g., TSS) tend to exhibit lighter δ^88/86Sr isotope compositions than those draining silicate-dominated terrains (HHCS) reflecting mass-balance between carbonate and silicate sourced Sr.

The marked increase in Sr/Ca ratios in the waters above the Sr/Ca ratio of the carbonate-dominated inputs in the TSS catchments is best modelled by balanced dissolution of bedrock Mg-calcite and re-precipitation of a low Mg-calcite. This avoids the necessity of postulating the very high initial Ca concentrations implied by simple precipitation of the secondary calcites modelled by Rayleigh fractionation and is consistent with the increase in Sr concentrations and approximately constant Ca concentrations with increasing Sr/Ca ratios in the carbonate-dominated TSS Marsyandi catchment. This conclusion is important for the calculation of silicate and carbonate chemical weathering rates in Himalayan catchments and the impact of the exhumation of the Himalayas on global climate (e.g., Kump et al., 2000). Most calculations of silicate and carbonate chemical weathering rates are based on ratios of some or all of the cations Na-K-Ca-Mg-Sr and ⁸⁷Sr/⁸⁶Sr ratios (e.g., Bickle et al., 2015; English et al., 2000; Galy & France-Lanord, 1999; Harris et al., 1998; Jacobson et al., 2002; Singh et al., 1998). The mechanism which elevates Mg/Ca and Sr/Ca ratios in the waters and its implication for magnitude of Ca inputs to the waters is critical to these calculations. The impact of solution-reprecipitation of calcites along groundwater flow paths is also dependent on how the flow paths sample silicate and carbonate rocks which adds further uncertainty to the calculations.

The limited change in δ^88/86Sr values with increasing Sr/Ca ratios is consistent with re-precipitation of secondary calcites at low rates such that the δ^88/86Sr fractionation factor and Sr/Ca partition coefficient are both small. These rates are consistent with field estimates of the rate of calcite re-crystallisation based on the flux of dissolved Ca out of the Marsyandi catchment, the amount of Ca exchanged by solution-re-precipitation and the likely surface area of calcite in the weathering zone. The low Δ^88/86Sr isotopic fractionation factors are also consistent with previously inferred Δ^44/42Ca calcite water fractionation factors (e.g., Z. Zhang & Wang, 2024). However, if these go to zero as calcite-water equilibrium is approached, the calcite re-precipitation rates imply that only a small fraction of the surface area of calcite in the weathering zone is recrystallising at any one time.

The calcite-re-precipitation rates are of the same order-of-magnitude as the rates of silicate mineral dissolution previously inferred from Li isotopic compositions (Bohlin & Bickle, 2019). These carbonate precipitation rates are presumed to be low because the solution-re-precipitation reactions take place at close to equilibrium which must contrast with the initial dissolution of calcite which rapidly raises calcite saturation in the groundwaters.

This data set adds to the growing database of riverine δ^88/86Sr calcite water fractionation factors and the utility of δ^88/86Sr, especially with regards to combining δ^88/86Sr with other non-traditional isotope systems (e.g., δ⁷Li, δ³⁰Si and δ²⁶Mg). Assessing characteristic Damköhler numbers for these isotope systems offers a rapid method for comparing reaction rates but more needs to be known about the reaction stoichiometries controlling the isotopic fractionations and on groundwater flow paths and mixing in catchments to be able to properly interpret the data.

Acknowledgments

We would like to thank Chris Pearce and Philip Pogge von Strandmann for their many constructive discussions regarding non-traditional stable isotopes and help with PHREEQC modeling, and Damien Calmels for constructive comments and feedback. We thank Geoff Nowell for help with TIMS measurements at Durham University and Fatima Mokadem for laboratory support at the University of Oxford. We would additionally like to thank all the patient colleagues, reviewers and editors who have provided much constructive feedback over the many years and many times we have submitted this paper. It would not be the paper it is today without their input. This work was supported by grants from UK Natural Environment Research Council, KWB & EIS by NE/F018126/1, ETT and MJB by NE/P011659/1, NE/N007441/1 and NE/V012037/1, and EIS and ETT by NE/T007214/1.

Author contributions

Emily Stevenson carried out the stable Sr-isotope and most of the geochemical analyses, wrote the first draft of the paper and led the various revisions. Kevin Burton and Ian Parkinson conceptualised and funded the research, supervising the writing of the manuscript and laboratory analysis. Rachael James and Basak Kisakürek collected most of the samples and supplied unpublished geochemical data on the samples, Ed Tipper & Emily Stevenson developed analytical methods for δ^88/86Sr at Cambridge, Mike Bickle developed the solution-precipitation model and derived the analytical solutions for the reactive transport modeling. All authors contributed to revising the many drafts of the manuscript.

Supplementary Information

https://doi.org/10.5285/ad233bd1-9e07-4729-bb3e-776e09a02a3a

Editor: C. Page Chamberlain, Associate Editor: Mark Albert Torres