Sedimentary Greigite Formation

1. Introduction

Greigite is the thiospinel of iron, Fe₃S₄. It has been described conventionally as a metastable phase due to the original solubility measurements of Berner (1967). Berner based his paradigmatic research on sedimentary pyrite (Berner, 1970b, 1984) largely on the basis of the results from this 1967 study. These results led to his insight into the fundamental role played by sedimentary pyrite in global biogeochemical cycles (e.g., Berner, 1982).

The assumption that greigite is a metastable phase in the Fe-S system has become a fundamental plank of various theoretical constructs ranging from pyrite formation processes to soil classification schemes. The measurements of Berner (1967) were discussed critically by Rickard and Luther (2007). The calculations of Berner (1967) were made with the older NBS value for the Gibbs energy ($\Delta_f G^{\circ}$) of aqueous ferrous ion (Fe²⁺_aq). Rickard and Luther (2007) updated these calculations and reported a lower value, which suggested that greigite is more stable than was originally thought. They suggested that their recalculated value was at the upper uncertainty limits for these measurements because it was not possible at that time to ensure that the greigite precipitate was free from contamination by mackinawite, the unstable tetragonal FeS_m. The mackinawite admixture increases the measured solubility of the precipitate and leads to underestimated greigite stability. The problem was based on the synthesis method, which involved precipitating mackinawite and then oxidizing and/or equilibrating it to greigite. The mackinawite to greigite translation is facile and is enabled by structural homology of the two phases (Lennie et al., 1995; Rickard & Luther, 2007; Yamaguchi & Katsurai, 1960). Pósfai et al. (1998a) examined greigite crystals with high-resolution electron micrography and found cryptic mackinawite interlayers within greigite crystals.

Progress on defining greigite stability was not possible until Li et al. (2014) developed a hydrothermal method for producing high-purity greigite involving cysteine as a S-source, as well as a surfactant, which avoided mackinawite formation. This enabled Shumway et al. (2022) to determine $\Delta_f G^{\circ}$ for greigite as -433.5 kJ mol^-1, which is more than 100 kJ mol^-1 less than older estimates (table 1). The consequence of these results is that greigite is a stable phase in the Fe-S system (Shumway et al., 2022; Subramani et al., 2020).

Greigite stability can be illustrated with respect to the stable iron sulfide phases pyrrhotite (represented as FeS_1.092) and pyrite:

$$\mathrm{Fe}_3\mathrm{S}_4=2.178 \mathrm{FeS}_{1.092}+0.822 \mathrm{FeS}_2\tag{1}$$

Shumway et al. (2022) reported entropy ($\Delta_r G^o_T$ in JK^-1 mol^-1), enthalpy ($\Delta_r H^{\circ}_T$ in kJ mol^-1), and Gibbs energy ($\Delta_r G^o_T$ in kJ mol^-1) values for reaction (1) for temperatures between 0 and 300 K (26.85 °C). Results for standard temperature and pressure (STP: i.e., 25 °C (298 K) and 1 atmosphere (0.1 MPa) pressure) are listed in table 2.

Figure 1.Evolution of reported Gibbs free energy estimates for greigite (ΔG^o_f in kJ mol^-1) with time (-290.4 (Berner, 1967), -308.3 (Rickard & Luther, 2007), -309.19 (Lemire et al., 2020), and -433.5 (Shumway et al., 2022)).

The large positive Gibbs energy for the reaction indicates that greigite is stable at 25 °C. The change in the measured Gibbs energy value for greigite is substantial (fig. 1) and we discuss here the implications of these results especially with respect to greigite formation and preservation in sedimentary environments and its relationship with other iron sulfides.

2. Methods

Equilibrium computations in this study were made by hand and with the ACT2 and RXN modules of the Geochemists Workbench™. Results are represented partially in pe-pH diagrams computed with the ACT2 algorithm. The negative logarithm of the electron activity, pe, was chosen over the potential relative to the hydrogen electrode, Eh (which is used in conventional Pourbaix diagrams) because the relationship between the computed Eh and that measured in sediments and natural waters with the Pt-calomel electrode combination is misleading in S systems. At best, the measured Eh reflects reactions in the S(0)-S(-II) system (Berner, 1964) and at worst it is the sum of partial redox potentials in the system. The relationship between pe and Eh is shown in equation (2):

$$\mathrm{pe}=-\log \mathrm{e}^{-}=\operatorname{Eh} F / 2.303 R \mathrm{T} \tag{2}$$

where F is Faraday’s constant, R is the universal gas constant, and T is temperature in K. At STP, equation (2) becomes pe = 16.9088 Eh and pe is converted readily to Eh by dividing by ~17.

The results of the equilibrium computations are described in terms of the total activities of dissolved iron (ΣaFe) and dissolved sulfur (ΣaS). The assumption that these activities approximate the concentrations is valid for aqueous solutions with ionic strengths up to 0.7 M, which is equivalent to fresh waters and seawater. At ionic strengths of 0.7 M, for example, the activity coefficient (γ_i) for H₂S (γ(H₂S)) is around unity, γ(HS^-) is 0.6, γ(Fe²⁺) and γ(SO₄^2-) are 0.2 (Rickard, 2012). This means that the error in equating concentrations with activities for iron and sulfur species in seawater is less than one order of magnitude. In solutions with ionic strengths greater than this, such as concentrated brines, activity coefficients for the species listed can vary by several orders of magnitudes. The approximation is then not valid and the relationship between concentrations and activity must be computed for each solution.

The challenge with considering phase stability in the Fe-S-H₂O system is the poor state of widely used thermodynamic databases especially with respect to sulfur species. Publication of Part 2 of the Organization for Economic Co-operation and Development (OECD) critical review of the chemical thermodynamics of iron has provided an invaluable resource of relatively up-to-date data on substances in this system (Lemire et al., 2020). Standard errors for thermodynamic values in the solubility and pe-pH diagrams presented here are usually within the thickness of the lines used in figures. When an uncertainty is egregious, as, for example, with pK₂(H₂S), the S^2-species is avoided in computations and is replaced by HS^-. However, it should be remembered that the listed data are ultimately based upon – or at least ground-truthed with – experimental data, which often have substantial uncertainties. Computational uncertainties are discussed in more detail below in sections 2.1 and 3.1. All results are presented for STP; i.e., 25 °C (298 K) and 1 atmosphere (0.1 MPa) pressure. Errors in extending these results to 50 °C are within the uncertainties of the thermodynamic data.

A conventional shorthand is used when describing relative stabilities, as used by Garrels (1960) in his pioneering introduction of Pourbaix-type equilibrium diagrams into geochemistry. Garrels’ insight was to realize that chemical equilibria in complex, multicomponent natural systems could be described in terms of pH and pe together with fixed activities of a few dominant species. For example, it may be stated that greigite is stable with respect to pyrite when, in fact, it is a group of components that determines relative stability. That is, greigite may be stable relative to pyrite in an assemblage containing a variety of aqueous and solid Fe-, S-, O-, and H- containing phases, which may be defined by the region of pe-pH space being considered.

2.1. Uncertainties

There has been no in-depth statistical analysis of the uncertainties generated by use of major computational chemical equilibrium algorithms, although studies have been made of individual thermodynamic parameters (e.g., Wanner & Östhols, 1999). The problem relates to error propagation through computations in relevant algorithms. This is likely to be far greater than the uncertainty in individual thermodynamic input parameters.

The standard error in thermodynamic data is usually listed as two standard deviations (2σ) mainly because it explains 95% of the variance (Wanner & Östhols, 1999). This is another expression of the “range rule” (Rickard, 2019). However, as noted by Wanner and Östhols (1999) and Wolery and Colon (2017), these estimates are not statistically rigorous, especially for single measurements; they rely more on professional judgements by experienced practitioners. The errors result primarily from thermodynamic input data uncertainties; further uncertainty is also developed in the computation, especially for predictions to different temperatures. Here, we present a simplistic uncertainty estimation for computing solubilities and pe-pH relationships of the more important phases in the greigite-centered Fe-S-H₂O system (table 3). The method used is simply to compute the root-mean-square error (RMSE) for the reaction Gibbs energy $\Delta_r G^{\circ}$ (kJ mol^-1) and consequent equilibrium constants (as log K) from reported $\Delta_f G^{\circ}$ uncertainty estimates for the species involved in the reaction. These values are compared with those listed by Lemire et al. (2020), which employ various methods.

We use the stoichiometric formula for greigite, Fe₃S₄, throughout so that units of mol^-1 greigite refer to moles of Fe₃S₄. For ease of computation, we use the reduced formulation Fe_0.75S when dealing with equilibria between greigite, pyrrhotite polymorphs, and smythite. Shumway et al. (2022) and the Geochemist’s Workbench™ data format both use the formula FeS_1.33 for greigite.

There has been longstanding interest in particle size effects on the relative thermodynamic stabilities of iron sulfides since Wolthers et al. (2003) and Ohfuji and Rickard (2006) defined the nanoparticle size of FeS_m (synthetic mackinawite-like) particles. Nanoparticles have high surface:volume ratios and, thus, the surface energy contribution to the free energy of a phase can be significant. Navrotsky et al. (2010) showed that observed surface energy differences in nanoparticles can shift metal/oxide redox free energies by 10-30 kJ mol^-1. Iron sulfide surface energies are not well known. Son et al. (2022) used density functional theory to estimate surface energies for mackinawite, greigite, and pyrite and found that for mackinawite and greigite they are, at least theoretically, potentially low enough to result in thermodynamic crossovers in their relative stabilities compared to pyrite in nanoparticles. However, the data are insufficiently precise to predict particle size contributions to the relative stability of greigite, or to evaluate the effect of estimated uncertainties in computations. The main effect of relative total free energy changes of sulfide nanoparticles may be mechanistic, related to nucleation, as suggested by the computations of Kitchaev and Ceder (2016) and Son et al. (2022)

3. Results

3.1. Estimated uncertainties

The thermodynamic data used here are listed together with the estimated uncertainties and data sources in table 3. The data include both experimentally measured data and derived data, which were selected by the various compilers. Data uncertainties are considered by Lemire et al. (2020) and all Gibbs energy values listed in table 3 are within their estimated ranges.

Shumway et al. (2022) reported that the estimated standard uncertainty in their experimental determinations is 0.01X, where X is the thermodynamic value. Thus, at 25 °C the free energy uncertainty for greigite is ± 0.627 kJ mol^-1. This would lead to estimated uncertainties in the computed log K of greigite reactions of ± 0.1 at STP. The error is compounded in determining the stability relationship between greigite and other phases by uncertainties intrinsic in the thermodynamic data for these phases. For example, Parker and Khodakovskii (1995) estimated the standard error for Δ_fG^o (Fe²⁺)_aq as ± 1 kJ mol^-1 and Lemire et al. (2020) estimated ± 0.641 kJ mol^-1. Three moles of Fe²⁺ are ultimately involved in the solubility of Fe₃S₄ (eq 3), so these estimates suggest that the Δ_fG^o (Fe²⁺)_aq uncertainty contributes a ~ ± 0.5 error in log K for the solubility. The error in Δ_fG^o (H₂S)_aq and Δ_fG^o (HS^-)_aq can be estimated from Suleimenov and Seward (1997) who reported an uncertainty of 0.02 in log K₁(H₂S), which is equivalent to ≤ ± 0.1 kJ mol^-1 for Δ_fG^o (H₂S)_aq and Δ_fG^o (HS^-)_aq. This compares with the value of ± 2.115 kJ mol-¹ estimated by Lemire et al. (2020).

Greigite solubility is expressed conventionally in terms of its solubility in acid solutions where orthorhombic sulfur, S⁰, is stable (eq 3):

$$\mathrm{Fe}_3 \mathrm{S}_4+6 \mathrm{H}^{+}=3 \mathrm{Fe}^{2+}+3 \mathrm{H}_2 \mathrm{S}+\mathrm{S}^0 \tag{3}$$

In the greigite stability areas, greigite solubility can be expressed by three equilibrium expressions (eqs 4–6):

$$\mathrm{Fe}_3 \mathrm{S}_4+16 \mathrm{H}_2 \mathrm{O}=32 \mathrm{H}^{+}+4 \mathrm{SO}_4 ^{2-}+3 \mathrm{Fe}^{2+}+30 \mathrm{e}^{-}\tag{4}$$

$$\mathrm{Fe}_3 \mathrm{S}_4+4 \mathrm{H}^{+}+2 \mathrm{e}^{-}=3 \mathrm{Fe}^{2+}+4 \mathrm{HS}^{-}\tag{5}$$

$$\mathrm{Fe}_3 \mathrm{S}_4+8 \mathrm{H}^{+}+2 \mathrm{e}^{-}=3 \mathrm{Fe}^{2+}+4 \mathrm{H}_2 \mathrm{S}\tag{6}$$

Greigite solubility is described by equation (4) in more oxidizing environments: it describes the locus of the upper, oxidized, greigite stability boundary. Greigite solubility in sulfidic solutions is described by equations (5–6). The RMSE for the greigite solubility from equations (4–6) is 3.1 kJ mol^-1, which is equivalent to an uncertainty in log K of 0.54. The greigite solubility uncertainty with respect to aqueous sulfate is affected by the estimated $\Delta_f G^{\circ}$ (SO₄^2-) uncertainty. Wolery and Colon (2017) estimated its total variation to be ± 0.418 kJ mol^-1 based on six values from major sources published between 1968 and 1995 with an average of -744.4 kJ mol^-1. They estimate the $\Delta_f G^{\circ}$ (H₂O) error to be ± 0.041 kJ mol^-1. Inserting these values into equation (4) suggests that the total log K uncertainty for the greigite solubility product in the sulfate stability field is ± 0.6 or < 0.3%.

The relative stability of greigite with respect to pyrite is described by equations (7–10). The interrelationship between greigite and pyrite in sedimentary systems can be expressed as a Fe²⁺-dependent reaction (eq 7) and two S(-II)-dependent reactions (eqs 8 and 9) and the reaction in the SO₄-field (eq 10):

$$\mathrm{Fe}^{2+} \ \mathrm{- \ dependent\ reaction}$$

$$2 \mathrm{FeS}_2+\mathrm{Fe}^{2+}+2 \mathrm{e}^{-}=\mathrm{Fe}_3 \mathrm{S}_4\tag{7}$$

$$\mathrm{S}(-\mathrm{II})\mathrm{-dependent\ reactions}$$

$$3 \mathrm{FeS}_2+2 \mathrm{H}^{+}+4 \mathrm{e}^{-}=\mathrm{Fe}_3 \mathrm{S}_4+2 \mathrm{HS}^{-}\tag{8}$$

$$3 \mathrm{FeS}_2+4 \mathrm{H}^{+}+4 \mathrm{e}^{-}=\mathrm{Fe}_3 \mathrm{S}_4+2 \mathrm{H}_2 \mathrm{S} \tag{9}$$

$$\mathrm{SO}_4(-\mathrm{II}) \text { dependent reaction }$$

$$3 \mathrm{FeS}_2+8 \mathrm{H}_2 \mathrm{O}=\mathrm{Fe}_3 \mathrm{S}_4+16 \mathrm{H}^{+} +12 \mathrm{e}^{-}+2 \mathrm{SO}_4 ^{2-}\tag{10}$$

The standard free energy of formation for pyrite measurements and estimates are summarized in table 4.

$\Delta_f G^{\circ}$ (FeS₂) was originally estimated experimentally by Toulmin and Barton (1964) who reported a value of -159.5 kJ mol^-1. A further independent experimental investigation by Grønvold and Westrum (1962) reported a value of -162.2 kJ mol^-1. Both sets of investigators reported a standard error of ± 2.1 kJ mol^-1. These results have been used widely in successive thermodynamic databases for computing $\Delta_f G^{\circ}$ (FeS₂) with a mean value of -160.2 ± 0.1 kJ mol^-1 (table 4). An outlier, which is excluded from the estimated mean, is the value of -166.9 kJ mol^-1 reported by Wagman et al. (1982), which resulted from use of an erroneous value for $\Delta_f G^{\circ}$ Fe²⁺(aq) (Rickard & Luther, 2007). Otherwise, the various derived values fall within the uncertainty limits reported by Toulmin and Barton (1964). The reasons for variation in the derived values have been discussed in detail by Wolery and Colon (2017). The value used here is -160.2 kJ mol^-1 because it is closest to the predicted value of the widely-used computed relationship between temperature and free energy (Helgeson et al., 1978). Its uncertainty is ± 2.1 kJ mol^-1.

Figure 2.Effect of variable $\Delta_f G^{\circ}$ (FeS₂) values between -162.3 kJ mol^-1 and -159.5 kJ mol^-1 on the computed pyrite-greigite stability boundary in pe-pH space at STP, ΣaS = 10^-3, and ΣaFe = 10^-6 (see text for details).

A sensitivity analysis indicates that $\Delta_f G^{\circ}$ (FeS₂) variations affect the pyrite-greigite boundary. In the Fe²⁺ reaction (eq 9), for example, it explains >75% of the variance. The RMSE is ± 4.4 kJ mol^-1 for this reaction, which gives a range of log aFe²⁺_aq values for the equilibrium reaction (7) of 0.8 log units. Pyrite-greigite equilibria in the sulfide field (eqs 8 and 9) have RMSE values of ± 6.3 kJ mol^-1, which leads to a ± 1.1 uncertainty in log K. This is equivalent to a pH uncertainty of ± 0.28 units. Similar results in the SO₄²-field (eq 10) are ± 6.4 kJ mol^-1 for $\Delta_r G^{\circ}$ and ± 1.1 for log K. This leads to a pH uncertainty for this reaction of < 0.1 pH units. The major effect is on the pyrite-greigite boundary in the HS^--dominant field of pe-pH diagrams (fig.2). The variation results in a slight pyrite stability zone increase if a lower $\Delta_f G^{\circ}$ (FeS₂) value is used.

3.2. Greigite solubility

There are two main reasons why greigite solubility is expressed in terms of its solubility in acid solutions where o⁠⁠r⁠⁠t⁠⁠h⁠⁠orhombic sulfur is stable (eq 3). First, greigite dissolution in acid was used by Berner (1967) in his original experimental determination of its stability. Second, greigite was thought to be a component of acid volatile sulfide, which is the source of H₂S gas that evolves on addition of acid to sulfidic soils and sediments. It, therefore, became important to distinguish the H₂S gas contribution that might be due to greigite or to mackinawite, which was also supposed to be a source of the evolved H₂S. If part of the iron sulfide sulfur is expressed as orthorhombic sulfur, then this would add uncertainties to the method. Cornwell and Morse (1987) showed that the stoichiometry of reaction (3) accorded closely with experimental results

Figure 3.Plot of the greigite solubility product (log aH₂S + log aFe²⁺) for reaction (3) at STP computed from the stability measurements of Shumway et al. (2022) compared to the original experimental data by Berner (1967) corrected using modern thermodynamic equilibrium data of Rickard and Luther (2007).

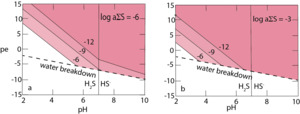
The logarithm of the equilibrium constant for reaction (3) at STP is –13.93; the reaction is independent of pe and highly dependent on pH (fig. 3). The effect of the revised stability data for greigite on its solubility product computed according to equation (3) is dramatic. The solubility product for greigite is some five orders of magnitude lower than was previously assumed. The solubility equilibrium expressed in reaction (3) is only valid for pe-pH regions where orthorhombic sulfur is stable. This is in acid solutions in areas bordering the S(-II)/SO₄(-II) couple boundary. The solubility product for greigite in acid environments, written as (aFe²⁺)(aH₂S), varies between around 10^-18 at pH = 7 to 10^-9 at pH = 2 (fig. 3). Greigite solubility in the sulfate field is shown in figure 4. The solubility gradient in this region is steep for solubility in a solution where the SO₄^2- activity is 10^-3 (similar to seawater). However, from inspection of equation (4) there is little change in greigite solubility in more dilute sulfate solutions in the micromolar range.

Figure 4.Greigite solubility in the sulfate field (log aSO₄²- = -3) from equation (5) with log aFe²⁺ boundaries between -12 and -9.

Greigite solubility is shown in figure 5 with respect to pH and pe in the sulfide field according to equilibrium equations (5) and (6). Results for total dissolved sulfide activities of 10^-3 and 10^-6 are shown equivalent to approximately millimolar and micromolar sulfide concentrations. In these representations, pyrite formation is suppressed for the kinetic reasons described above. Thus, greigite solubilities are generally equivalent to sub-nanomolar aqueous Fe²⁺ concentrations in sulfidic environment.

Figure 5.Greigite solubility in the sulfide region at the logarithms of the total dissolved sulfide activities of (left) log a ΣS(-II) = -6 and (right) log aΣS(-II) = -3 for aqueous Fe activities of 10^-6, 10^-9, and 10^-12 (-6, -9, -12) according to equations (5) and (6).

3.3. Greigite stability relationships

Equilibrium relationships between sulfur species and greigite and pyrite, in terms of pe and pH, for sulfur species concentrations in the mM and μM ranges and dissolved Fe concentrations in the μM and nM ranges are shown in figure 6.

Figure 6.Equilibrium stability relationships between pyrite and greigite in terms of pe and pH for total dissolved S concentrations (total dissolved sulfur species activity, ΣaS, see text) on the (left) mM and (right) μM ranges and total dissolved Fe (total dissolved Fe species activity, ΣaFe, see text) in the μM (6B and 6E) and nM ranges (6C and 6F). Equilibrium relationships for dissolved S species are shown in 6A (ΣaS = 10^-3) and 6D (ΣaS = 10^-6) and their stability is indicated with dashed lines in 6B, 6C, 6E and 6F. Goethite is substituted for the stable Fe oxide phases hematite, maghemite, and magnetite, and the Green Rusts are suppressed.

From these results, greigite is stable with respect to pyrite over large parts of pe-pH space and pyrite is stable with respect to greigite in more acid environments. Closer inspection of figure 6 indicates, however, that for millimolar total dissolved S concentrations, pyrite occupies much of the key area around pH = 6-8.

The stability zone for the iron oxyhydroxide, goethite, is indicated in figure 6. This is achieved by suppressing the more stable iron oxides (hematite, magnetite, and maghemite), which would otherwise occupy similar pe-pH space. Goethite is preferred here because there is considerable interest in it as a potential reactant in sedimentary iron sulfide formation (e.g., Peiffer et al., 2015) and as an oxidation product of greigite. As shown in figure 6, greigite, like pyrite, has a small but significant stability region in the sulfate-dominated area of pe-pH space that otherwise might be regarded as relatively “oxidized”. The dissolved S(-II) species activity decreases logarithmically above the boundary where aSO₄^2- and aΣS(-II) are equal (fig. 6A, D). Likewise, the green rust minerals, complex double salts of Fe^IIFe^III oxyhydroxides and sulfate, carbonate, and chloride, and an apparent natural mineral equivalent, fougerite, are not represented here because thermodynamic data for these compounds are uncertain. However, as pointed out by Rickard and Luther (2007) these materials could have significant metastability, or even stability, in such systems.

Marcasite is not considered here because its relationship with other iron sulfides is uncertain (e.g., Kitchaev & Ceder, 2016; Luther et al., 2003; Schoonen & Barnes, 1991a). The marcasite-greigite association has not been reported from sediments, which may be a result of relative greigite solubility in the acidic environments in which marcasite forms.

3.4. Greigite-pyrite equilibria

The interrelationship between greigite and pyrite in sedimentary systems can be described by equations (7–10). The S(-II)-dependent reactions describe the equilibria in terms of H₂S(aq) and HS^- and are, therefore, pH dependent with reaction (8) dominating in alkaline regimes and reaction (9) dominating in acidic environments. Equation (10) describes the greigite-pyrite boundary in more oxidizing environments such as those commonly found near the sediment-water interface in modern environments. These reactions are chemical bookkeeping exercises and have no relationship with actual mechanisms; that is, they bear little or no relationship with the chemical processes involved in the equilibrium between pyrite and greigite. From the equilibrium data, greigite does not necessarily form before pyrite: pyrite can be replaced by greigite if conditions facilitating pyrite dissolution occur or greigite overgrowths can form on pyrite if sedimentary pe-pH conditions change (cf. Burton et al., 2011).

In figures 6E and F greigite dominates pe-pH space in the sulfide stability regions at lower total dissolved S concentrations whereas pyrite becomes more significant at higher total dissolved S concentrations (figs. 6B and C). The effect of dissolved Fe concentrations on pyrite-greigite relationships become more pronounced at lower total dissolved S concentrations (figs. 6E and F). In low total dissolved S environments, solubility relationships result in the greigite stability zone expanding into more acidic environments (figs. 6E and F) so that it is the dominant iron sulfide over large swathes of pe-pH space, even in more acid environments.

Although pyrite tends to be stable in more oxidized environments near the sulfide-sulfate boundary, greigite has a small but significant stability zone subjacent to this boundary. Overall, however, greigite tends to dominate pe-pH space in lower pe environments (colloquially known as highly reduced) and is dominant in sediments with pe values adjacent to the water stability boundary.

3.5. Greigite-pyrrhotite relationships

“Pyrrhotite” is a portmanteau term that includes several non-stoichiometric $\mathrm{Fe}_n \mathrm{S}$ polytypes, (0.866< n <0.931), and troilite (n = 1.000). Conventionally, the composition is written as $\mathrm{Fe}_{(1-x)} \mathrm{S}$ (where (1-x) ≡ n) or $\mathrm{Fe}_{(z-1)} \mathrm{S}_{\mathrm{z}}$ ( z ≥ 8 and n ≡ (z-1)) but these lead to ungainly representations in equilibrium chemistry and we use the $\mathrm{Fe}_n \mathrm{S}$ formulation here for clarity. Pyrrhotite is a stable mineral in the Fe-S system and it forms together with pyrite from the thermal breakdown of greigite. The pyrrhotite polymorphs are commonly referred to in terms of multiples of the c-axis (NC) superstructures that arise through the Fe vacancy distributions that result from the non-stoichiometry (Elliot, 2010). Apart from troilite 2C (FeS), four pyrrhotite polytypes are apparently stable including 6C (Fe_0.917S), 11C (Fe_0.909S), 5C (Fe_0.900S), and 4C (Fe_0.875S) pyrrhotite (Jin et al., 2021). The 5C, 6C, and 11C pyrrhotites, collectively known as the hexagonal pyrrhotites, are not ferrimagnetic, but commonly coexist with the ferrimagnetic 4C or monoclinic pyrrhotite. Also, several metastable polytypes exist as intergrowths with stable pyrrhotites where N is not an integer.

The generic relationship between greigite (Fe_0.75S) and the pyrrhotites (Fe_nS) can be described by equation (11).

$$\mathrm{Fe}_{0.75} \mathrm{S}+(n-0.75) \mathrm{Fe}^{2+} +2(n-0.75) \mathrm{e}^{-}=\mathrm{Fe}_n \mathrm{S}\tag{11}$$

$$\log K=2(n-0.75) \mathrm{pe}-(n-0.75) \log a\left(\mathrm{Fe}^{2+}\right)\tag{12}$$

In equation (12), the equilibrium constant, K, which describes the stability boundary between greigite and the pyrrhotites, can be described solely in terms of the logarithm of the activity of aqueous Fe² (log a(Fe²⁺)) and pe; it is independent of the dissolved S activity (eq 12). As the aqueous Fe²⁺ activity increases, the pe value for the boundary increases. Likewise, for any given pyrrhotite composition, $\mathrm{Fe}_n \mathrm{S}$, the pe boundary value increases with increasing n, which means that stoichiometric FeS is the most stable phase. The lower stability limit for water is pe = - pH, so the pyrrhotites can only appear on the pe-pH stability diagrams in figure 6 where pe > -10. Recommended values for the Gibbs energies of the pyrrhotites are limited to the 2C (FeS), 4C (Fe_0.875S), and 5C (Fe_0.9S) polytypes (Lemire et al., 2020), which have no pe stability boundaries > -10 at STP, so they have no stability region relative to greigite in normal sediments. This confirms the conclusion of Rickard and Luther (2007) but is contrary to the finding of pyrrhotite stability using the older greigite metastability data (e.g., Turney et al., 2023).

Equilibrium relationships between the pyrrhotites and greigite can be written in terms of the dissolved S activity. For example, the equilibrium relationship between monoclinic 4C pyrrhotite, Fe_0.875S, and greigite in the HS^- field and the computed value of the logarithm of the equilibrium constant, log K, at STP, is given by equation (13):

$$\begin{aligned} &0.857 \mathrm{Fe}_{0.875} \mathrm{S}+0.143\mathrm{HS}^{-}\\ &=\mathrm{Fe}_{0.75} \mathrm{S}+0.143 \mathrm{H}^{+}+0.286 \mathrm{e}^{-} \\ &\qquad \log K=4.731 \end{aligned} \tag{13}$$

The result confirms that the pyrrhotites have no stability relative to greigite in sediments.

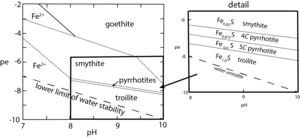
The relative stability of the pyrrhotites and troilites is shown in figure 7. In this diagram, the stable phase greigite is suppressed to allow relationships among the metastable pyrrhotites to be revealed. Boundaries between the various metastable phases are indicated by dotted lines to emphasize uncertainties in the values of thermochemical data used (table 3). However, they clearly indicate the decreasing pe trend with increasing Fe:S ratio for these phases and demonstrate that these phases are more probable in extremely reduced environments at or below the water stability boundary.

Figure 7.Metastability regions of smythite and the pyrrhotites in the absence of greigite in terms of pe-pH for ΣaS = ΣaFe = 10^-6 from estimated thermodynamic data. An expanded view is shown of the detailed relative stability trend, with decreasing pe for increasing Fe:S ratio.

3.6. Greigite-smythite relationships

Smythite is a poorly defined phase that was originally given the composition Fe₃S₄ (Erd et al., 1957). It was shown to be a pure mineral in the binary Fe-S system by Rickard (1968a) although there was a brief interlude when it was mistakenly reported to be an iron-nickel sulfide, (Fe,Ni)₉S₁₁ (Taylor & Williams, 1972). Since the original definition there have been various representations of its stoichiometry (e.g., Fe₁₃S₁₆ (Fleet, 1982)) although current consensus is that its composition is Fe₉S₁₁ or Fe_0.82S (e.g., Furukawa & Barnes, 1996; Horng et al., 2020). However, it is probable on crystallochemical grounds that its composition varies. The relationship between greigite and smythite can be described by equation (14).

$$\mathrm{Fe}_{0.75} \mathrm{S}+0.07 \mathrm{Fe}^{2+}+0.14 \mathrm{e}^{-}=\mathrm{Fe}_{0.82} \mathrm{S}\tag{14}$$

For smythite to have any stability region with respect to greigite in sediments, its Gibbs energy would have to be close to that of greigite (-108 kJ mol^-1 as Fe_0.75S) because their compositions are similar. As is the case for the pyrrhotites, the lower stability limit for smythite in terms of pe would need to be > -10 for it to appear on the pe-pH diagrams in figure 6. The stoichiometry of equation (14) suggests that the standard Gibbs energy of formation for smythite, Fe_0.82S, would need to be < -115 kJ mol^-1 for it to have a stability region relative to greigite, Fe_0.75S, in sediments. The Gibbs energy of smythite is unknown. Lemire et al. (2020) concluded that its lower limit, based on the Fe₉S₁₁ formulation, is 1014 ± 19 kJ mol^-1. This is equivalent to -92.18 ± 1.73 kJ mol^-1 for Fe_0.818S. However, Lemire et al. (2020) computed this limit based on the breakdown of smythite to Fe_0.857 S and pyrite assuming that greigite was metastable.

Lemire et al. (2020) showed that the enthalpies of formation for five pyrrhotite polytypes correlate linearly with the mole fraction of Fe. This translates to a linear relationship between Gibbs energy values for the pyrrhotites and their Fe:S ratios. Extending this to a pyrrhotite composition equivalent to that of smythite, Fe_0.82S, would give $\Delta_f G^{\circ}$ (smythite) = -95.10 kJ mol^-1, which is below the lower limit computed by Lemire et al. (2020). We use this value to indicate the metastability region of smythite in terms of pe-pH in figure 7. As expected, its metastability region is at higher pe values than for the pyrrhotites and occupies a larger pe-pH space.

4. Discussion

4.1. Greigite distribution in sediments

Establishment of greigite as a stable Fe-S phase has far-reaching consequences for explaining its sedimentary distribution. When greigite was thought of as a metastable phase – especially as a necessary precursor to pyrite – interpretation of its sedimentary occurrence was often complex. Greigite preservation in older sediments and sedimentary rocks was also problematic. The distribution of greigite in pe-pH space (fig. 6) brings further insights into the factors that control its sedimentary distribution.

Greigite has been shown to be a common minor accessory mineral in sediments since it was first described, as melnikovite, by Doss (1912), from Miocene sedimentary rocks and subsequently by Volkov (1961) from Black Sea sediments. Its type locality is a Tertiary lacustrine sequence in San Bernadino County, California (Skinner et al., 1964). It has also been reported widely from methanic sediments, freshwater sediments, and marine sediments (e.g., Roberts, 2015). Rickard (2012) concluded that greigite is particularly associated with freshwater sediments, especially lacustrine sediments. Lin et al. (2023) also reported that it is common in lake sediments. Original greigite synthesis protocols, which reported that low pH promotes greigite formation (e.g., Yamaguchi & Wada, 1972), seemed consistent with this observation. However, the pe-pH stability region of pyrite relative to greigite in figure 6 decreases with decreasing total dissolved S concentration for the same total dissolved iron concentrations. Thus, relatively dilute sulfate freshwater systems are likely to be responsible for greigite formation in freshwater sediments, rather than the lower pH directly.

Greigite is also reported in marine sediments. It parallels pyrite in being distributed more widely in nearshore sediments than in pelagic sediments, for the same reasons: there is generally a relative lack of organic matter in pelagic sediments with consequent low sulfide production. Greigite is also reported from hemipelagic marine environments (e.g., Liu et al., 2004). By contrast, pelagic sediment occurrences are infrequent and related to special circumstances, such as the iron-enriched Amazon fan sediments (Kasten et al., 2004).

Kao et al. (2004) concluded that elevated total dissolved iron concentrations combined with low S concentrations facilitate sedimentary greigite formation. The requirement for relatively high dissolved Fe:S ratios for greigite formation is consistent with its frequent occurrence in freshwater sediments and its limited number of reports from pelagic sediments. This is consistent with the stability data (fig. 5), which indicate that greigite occupies a larger proportion of pe-pH space relative to pyrite as dissolved Fe concentrations increase and dissolved S concentrations decrease.

Sedimentary greigite occurrences are common in transitional environments, particularly freshwater ↔︎ marine settings. This was originally suggested by Berner (1970a) for Black Sea sediments. Strechie et al. (2002) reported that greigite occurs consistently in horizons that mark the freshwater to marine transition in the Black Sea. Greigite has been reported widely in sediments from brackish environments, particularly from seas that have been isolated from the open ocean such as the Caspian Sea (Jelinowska et al., 1998), Baltic Sea (Sternbeck & Sohlenius, 1997), and Black Sea (Volkov, 1961). It has also been reported from lakes that have experienced marine incursions (e.g., Snowball & Thompson, 1990; Wang et al., 1999) and in transitional lake sediment facies from which greigite occurrences have been used to track lake environmental changes (e.g., Fu et al., 2015; W. Li et al., 2019; Roberts et al., 1996). Greigite occurs in the Santa Barbara Basin in intervals with enhanced iron contents associated with increased terrigenous run-off (Blanchet et al., 2009), in continental shelf sediments where pore fluid compositions changed with sea-level variations (e.g., Oda & Torii, 2004), and in tidally re-flooded wetlands in NE Australia (Burton et al., 2011). Greigite is also reported from near-shore marine environments with varying water freshness, especially estuaries (e.g., Chen et al., 2015; Hallam & Maher, 1994; Mohamed et al., 2011). As shown in figure 6, greigite formation is enhanced in environments with low total dissolved S and high dissolved Fe concentrations. Many of the above examples are consistent with greigite formation associated with exposure of relatively Fe-rich freshwater systems to rising sulfate concentrations during marine transitional events or when sulfate-rich waters are diluted by freshwater influxes.

Greigite was first reported from soils by Stanjek et al. (1994) from a Bavarian gley soil developed on colluvium. Soil and wetlands are further examples of systems subject to rapid environmental change but, in this case, from water-saturated, often sulfidic, systems to water-undersaturated, often oxygenated, systems (Roberts, 2015) which means that oxygen-sensitive sulfide phases like greigite can form and be destroyed repeatedly during soil development.

Relating greigite distributions to sedimentary environment is complex. Greigite forms in both stable sedimentary systems and in transitional horizons that reflect changing environments. Furthermore, it can form at any time during sedimentary history, from formation in the water column (e.g., Cutter & Kluckhohn, 1999) through to late diagenesis (e.g., Kars et al., 2021), if the necessary reactants are present (Roberts, 2015). This means that greigite within a given sediment may not relate to its depositional environment; rather, it may have formed in a completely different environment during subsequent sedimentary history (e.g., Reynolds et al., 1994).

A genetic connection between methane and greigite was suggested by Kasten et al. (1998) from methanic Pleistocene-Holocene Amazon fan sediments at 3500 m water depth. Greigite has since been reported widely in methanic sediments and cold seeps. It has been suggested that the greigite-pyrrhotite (smythite)-siderite association may be a marker of methanic (paleo)-environments (e.g., Horng et al., 2020; Rudmin et al., 2018). Greigite forms from the sulfide produced during anaerobic methane oxidation reacting with iron species in current or ancient sulfate-methane transition zones (e.g., Amiel et al., 2020; Badesab et al., 2019; Enkin et al., 2007; Horng & Chen, 2006; Housen & Musgrave, 1996; Larrasoaña et al., 2007; Musgrave et al., 2006). Greigite occurrences in these zones are consistent with figure 6, where greigite is stable relative to pyrite at lower pe values near the water stability zone where methane generation dominates. Greigite formation relative to pyrite may be enhanced if dissolved Fe²⁺ concentrations increase in the methanic zone (Beal et al., 2009) leading to increased dissolved Fe:S ratios.

4.2. Greigite distributions in organisms

The dependence of much of the S in sedimentary greigite on the products of sulfate-reducing prokaryotes means that there is, a priori, a close relationship between greigite and organisms. Freke and Tate (1961) reported a magnetic iron sulfide in cultures of sulfate-reducing bacteria and Rickard (1968b) first identified greigite in bacterial products. Early reports of greigite occurrences in plant vacuoles (e.g., Jedwab, 1967; Morse & Cornwell, 1987) appeared consistent with these experimental results and led to suggestions that greigite forms preferentially in such microenvironments. However, it is more probable that enclosed environments prevented greigite oxidation, as suggested by Krupp (1994) with reference to greigite occurrences within siderite.

The breakthrough in understanding the close relationship between greigite and organisms came with discovery of magnetosomal greigite in magnetotactic bacteria (Farina et al., 1990; Mann et al., 1990; Pósfai et al., 1998a, 1998b). Magnetotactic prokaryotes, including both bacteria and multicellular organisms, are ubiquitous in sulfidic sediments, but the distribution of greigite producers compared to the more widely identified magnetite producers is unclear. Putative reports of greigite magnetofossils in ancient sedimentary rocks remain rare (Bai et al., 2022; Chang et al., 2014; Pósfai et al., 2001; Vasiliev et al., 2008). The challenge in understanding magnetotactic greigite includes its preservation and how it forms, particularly in preference to pyrite. Our results suggest that greigite magnetofossils can be preserved geologically, although this will be limited by post-mortem cell lysis (Rickard, 2012) and subsequent oxidation and dissolution of exposed greigite nanoparticles. Lefèvre et al. (2011, 2013) identified the gene sequences that lead to magnetosomal greigite production and showed that, compared to magnetite-producing magnetotactic bacteria, greigite-producers contain a second set of magnetosome gene clusters. Greigite nucleation is, thus, biologically-regulated and occurs at specific magnetosome membrane sites (Komeili et al., 2006). Pósfai et al. (1998b) showed that magnetosomal greigite develops from original mackinawite, which is consistent with greigite stability. The fact that greigite is a stable Fe-S phase also explains why these organisms can maintain greigite in their organelles without it converting to pyrite.

Greigite-pyrite relationships

Berner (1974) suggested two distinct sedimentary pyrite formation routes: (1) between FeS_m (mackinawite) and sulfur (eq 15) and (2) between greigite and sulfur (eq 16).

$$\mathrm{FeS}+\mathrm{S}^{\circ}=\mathrm{FeS}_2 \tag{15}$$

$$\mathrm{Fe}_3 \mathrm{S}_4+ 2 \mathrm{S}^{\circ}=3 \mathrm{FeS}_2\tag{16}$$

The Gibbs energy for reaction (16) is -53.4 kJ mol^-1 (where S is approximated by the orthorhombic polymorph) and greigite has no stability with respect to pyrite and S. This is significant because the S stability region is sensitive to total dissolved S activity (fig. 6A and D). However, this reaction only occurs within the S stability region. Outside this region, pyrite stability with respect to greigite is defined by reactions (7-10). Schoonen and Barnes (1991c) coupled the two separate reactions (15) and (16) proposed by Berner (1974) and mistakenly suggested that pyrite forms via equilibrium transformations of initial mackinawite (tetragonal FeS) to greigite (cubic Fe₃S₄) and ultimately to pyrite (FeS₂). The mackinawite → greigite → pyrite equilibrium sequence became a false paradigm for pyrite formation in the latter 20^th century. One reason for this conclusion is that the mackinawite → greigite equilibration is facile and results in synthetic greigite often containing relict mackinawite (Pósfai et al., 1998b). The process may be the major route for sedimentary greigite formation.

Rickard and Luther (2007) showed that contamination of synthetic greigite by highly metastable FeS_m is the main cause of the underestimated greigite stability by Berner (1967). Experimentally, dissolved iron and sulfide concentrations are necessarily high to collect sufficient pyrite product, which leads to nucleation of unstable, mackinawite-like FeS_m forms. These often equilibrate rapidly, at least partially, to form greigite so that it appears to the experimentalist that greigite is involved in pyrite formation. Rickard et al. (2001) showed that, in the presence of aldehydic carbonyl, pyrite formation is inhibited and that greigite forms. Inhibition of mackinawite formation using cysteine as a S source led ultimately to synthesis of pure, mackinawite-free greigite (G. Li et al., 2014). This, in turn, finally enabled greigite stability estimation.

The “formation of pyrite” involves two processes, nucleation and crystal growth. Pyrite nucleation is often inhibited by the required large critical supersaturations, which range from 10¹¹ to 10¹⁵, depending on the presence or absence of suitable catalytic surfaces (Rickard & Luther, 2007). The more extreme supersaturations can lead to burst nucleation, especially in homogenous systems (Rickard, 2021; Schoonen & Barnes, 1991b). Heterogeneous nucleation requires lower supersaturations and is ultimately the pyrite crystal growth mechanism. As with any iron- and/or sulfur-containing mineral, greigite can be a reactant for pyrite formation, just as pyrite can be a reactant for greigite formation. As with other Fe compounds, such as mackinawite and iron oxyhydroxides, greigite dissolves (e.g., equations (3­–6)) and pyrite nucleates homogeneously, or heterogeneously on a mineral or organic matter surface. There is little published evidence for pyrite nucleation on greigite surfaces although this should be possible. As shown by Rickard (2021) the common factor in pyrite nucleation and crystal growth is the availability of FeS moieties, including surface <FeS> groups, and it is probable that <FeS> groups occur on greigite surfaces.

4.3. The greigite-pyrrhotite-smythite association

As shown in figure 6, although various pyrrhotite polymorphs are stable phases in the Fe-S system, they have no stability region in pe-pH space in sediments relative to greigite and pyrite. The implication is that, at equilibrium, sedimentary pyrrhotites will dissolve and re-react with dissolved Fe species to produce greigite within large swathes of pe-pH space. Horng and Roberts (2006) noted that authigenic pyrrhotites have been reported from sediments and sedimentary rocks, although many sedimentary 4C pyrrhotites are likely to be detrital in origin. Burgeoning reports of authigenic pyrrhotite are now recognized to be associated with methanic sediments where they often co-exist with greigite (e.g., Horng, 2018; Larrasoaña et al., 2007; van Dongen et al., 2007). The pyrrhotite-greigite-siderite association has been proposed as an indicator of methanogenesis in ancient environments (Rudmin et al., 2018), with the added caveat that pyrrhotite may have been mistakenly identified as smythite, rhombohedral Fe_0.82S (Horng et al., 2020).

The upper thermal stability limit of smythite is reported to be 65 °C (Taylor, 1970), so smythite can be preserved in sediments. Thermodynamic analysis (fig. 7) suggests that it is likely to form, metastably or stably, at extremely low pe conditions near the lower water stability boundary in alkaline conditions, which is consistent with its presence in methanic sediments. Furukawa and Barnes (1996) concluded that smythite is metastable and that its formation is due to mechanistic factors. Close association of natural smythite occurrences in sediments with siderite (Horng et al., 2020) suggests that reaction with this mineral may play an important role in smythite formation, possibly structurally facilitated, as suggested by Rickard (1968a).

5. Conclusions

Thermodynamic analysis of the Fe-S system using revised stability data for greigite indicates that the major controls on sedimentary greigite distributions are the relative concentrations of dissolved sulfide and iron species. This is consistent with the conclusion of Kao et al. (2004) based on geochemical analysis of greigite-bearing sediments. Sulfide must be present, which usually correlates to organic matter availability and aqueous sulfate concentration. High relative dissolved iron concentrations play a major determinative role in greigite formation relative to pyrite, as illustrated by widespread greigite occurrences in lake and iron-enriched marine sediments, where sulfate generally has lower concentrations. This is likely the main cause of greigite formation in freshwater sediments.

Greigite can form at any time during the sediment history if conditions for its prevalence over pyrite are satisfied. These mainly relate to relatively high sulfate to iron ratios and low pe in the aqueous medium. Greigite formation may, thus, document paleoenvironmental changes in the sediment, including episodes of methanogenesis.

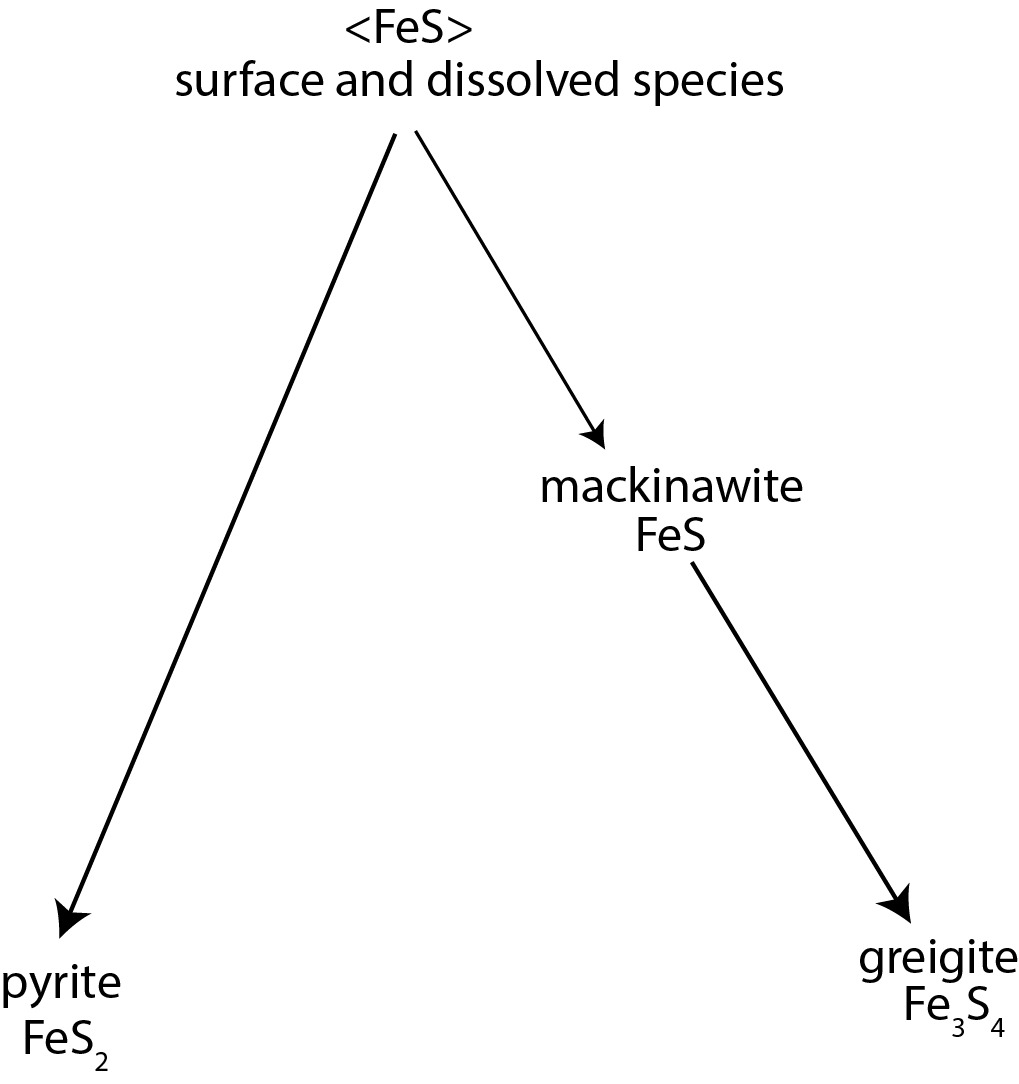
Interrelationships between the more abundant sedimentary iron sulfides are outlined in figure 8. <FeS>, the FeS moiety that occurs in various forms in sedimentary environments, is a necessary reactant for pyrite nucleation in solution or on mineral surfaces; nucleation on pyrite surfaces is its main crystal growth route. <FeS> includes aqueous FeS clusters, which are widespread in sulfidic environments (with embryo tetragonal (i.e., mackinawite-like) structures). Various workers have proposed other short-lived nanoparticulate FeS phases, mainly based on computational modeling, during mackinawite structure evolution. Mackinawite is metastable and equilibrates to greigite. Although greigite can be synthesized via diverse protocols, its formation in sedimentary environments and organisms appears to be mainly via mackinawite equilibration.

Figure 8.Current understanding of major interrelationships between sedimentary sulfides. <FeS> describes FeS moieties in solution, such as aqueous clusters, and on mineral surfaces.

In this scheme, greigite is an end-product. As a stable phase, it does not equilibrate further to produce other iron sulfides such as pyrite. This explains the accumulation of considerable incompatible theoretical, experimental, and observational evidence regarding pyrite and greigite. For example, pyrite can form at > 300 °C where greigite may not exist, there is no structural homology between greigite and pyrite, pyrite crystal growth occurs with no evidence for greigite involvement, the size of greigite and pyrite critical nuclei are incompatible, and no greigite is detected in many pyrite syntheses. There are also incompatibilities in natural systems (e.g., Howarth, 1979; Perry & Pedersen, 1993; Rickard & Morse, 2005), including a widespread lack of sedimentary greigite compared to pyrite. The explanation that all greigite has converted to pyrite is a false paradigm. Burton et al. (2011) concluded that pyrite formation is decoupled from greigite formation. They found no evidence for pseudomorphic greigite replacement by pyrite or for pyrite growth via oriented aggregation of greigite crystals.

Authigenic pyrrhotite and smythite are missing from figure 8 because their relationships with greigite are unknown. Both are reported to coexist with greigite and siderite in methanic sediments, but the revised greigite stability data suggest that both are unstable with respect to sedimentary greigite. It is, therefore, possible that the reported association with greigite is metastable and is a snapshot of an equilibration process, or that we do not yet have adequate thermodynamic parameters for smythite or relevant pyrrhotite polytypes. Association of these phases with methanic sediments is consistent with existing thermodynamic data. Many reports of authigenic pyrrhotite may also refer to smythite; the smythite (pyrrhotite)-siderite association in sedimentary rocks may be a paleoenvironmental indicator of past methanic events. Smythite (pyrrhotite) forms by direct reaction with siderite and its formation is mechanistically facilitated by homologies between siderite and smythite crystal structures, which bypasses the conventional <FeS> → mackinawite route outlined in figure 8.

ACKNOWLEDGMENTS

This contribution is dedicated to the memory of the late great Bob Berner in recognition of the major contribution he made to understanding sedimentary iron sulfide geochemistry. The title of this paper deliberately echoes the title of Bob’s epoch-making 1970 paper, Sedimentary Pyrite Formation, which was also published in this journal. We thank Manuel Scharrer, Kristina Lilova, Brian Woodfield, Tamilarasan Subramani, and Kurt Leinenweber for comments during manuscript preparation. Mark Dekkers and an anonymous referee made valuable comments on an original draft of the paper. We thank the Associate Editor for his support and encouragement during preparation and submission of this contribution.

AUTHOR CONTRIBUTIONS

D.R. designed the study and performed the computations. All co-authors contributed to writing the paper.

Editor: C. Page Chamberlain, Associate Editor: Timothy W. Lyons