The Rare Earth Element Distribution in Marine Carbonates as a Potential Proxy for Seawater pH on Early Earth

1. INTRODUCTION

Seawater pH is one crucial yet unconstrained environmental parameter relevant to the early climate and evolution of life. Marine pH is important because it is directly connected to the partial pressure of CO₂ in the atmosphere (pCO₂), which was likely a key greenhouse gas in the Precambrian that controlled Earth’s surface temperature (Catling & Zahnle, 2020; Sleep & Zahnle, 2001; Walker et al., 1981). In aquatic chemistry, pH is a “master variable” because it commonly defines whether chemical reactions are favored and provides biogeochemical context (Konhauser & Riding, 2012; Meador, 1991). Additionally, seawater pH is an essential parameter for the origin of life, e.g., in trans-membrane proton gradients (Lane et al., 2010).

Constraints on Precambrian seawater pH are very sparse and debated (see summary in Krissansen-Totton et al., 2018). For example, Grotzinger and Kasting (1993) estimated that Precambrian seawater had a slightly acidic to alkaline range of pH 5.7–8.6 based on the absence of calcium sulfate minerals. Pinti (2005) argued for a pH as low as 4.8 in the Hadean because of higher atmospheric CO₂, although Kadoya et al. (2020) constructed a global carbon cycle model where the Hadean ocean was quasi-neutral or slightly alkaline. In contrast, some have argued that the Archean ocean was highly alkaline with a pH of 9–11, similar to modern soda lakes (Kempe & Degens, 1985; Kempe & Kazmierczak, 2011).

Evolving seawater chemistry models have estimated the evolution of pH rising from slightly acidic to quasi-neutral over 4.0 billion years. Halevy and Bachan (2017) modeled the dissolved ion changes in seawater under an assumed stable climate showing that the average pH has likely risen (on average) over time since the Archean. Krissansen-Totton et al. (2018) estimated pH using a self-consistent carbon cycle climate model different from Halevy and Bachan (2017), but reached similar conclusions reflecting a secular decrease in atmospheric pCO₂. However, lower pCO₂ levels from acid weathering of impact ejecta can also create a slightly alkaline ocean in the early Archean and Hadean (Kadoya et al., 2020).

Consistent seawater pH proxies would constrain the wide range of pH estimates of early Earth. A rough proxy of 1–2 pH units would be sufficient for telling the difference between acidic, neutral, or alkaline seawater.

One candidate for a seawater pH proxy is the rare earth element (REE) distribution. REEs include the 15 lanthanide elements (La - Lu), Scandium (Sc) and Yttrium (Y). The REEs we discuss in this paper are the 15 lanthanide elements that have similar chemical properties. Rare earth elements exist in modern seawater at part per trillion concentration and are divided into two groups, Light REEs (La-Sm, LREEs) and Heavy REEs (Gd-Lu, HREEs), based on their atomic number and chemical behavior (Elderfield & Greaves, 1982; McLennan & Ross Taylor, 2012). Some also define Sm-Ho as the Middle REEs (MREEs; Rollinson, 1993; Y. Zhao et al., 2022). Besides the 15 lanthanides, Y is commonly included in the analysis because of its similarity to the lanthanides (Bau, 1999).

When analyzing REEs in seawater and marine sediments, we normalize REE concentrations by shale, typically the Post Archean Australian Shale (PAAS, see Pourmand et al. (2012)).

$$m_{i} = \frac{M_{i}}{k_{i}}\tag{1}$$

Here, m_i is the concentration of REE with an atomic number i normalized by shale (unitless), M_i is the molal concentration of measured REE i in seawater or marine sediments (mol/g), and k_i is the molal concentration of the REE in the shale (mol/g). Shale-normalization removes the Oddo-Harkins effect, a result of cosmic nucleosynthesis, in which elements with even atomic numbers are usually more abundant because elements with odd atomic numbers capture protons more easily, creating a zigzag pattern when unnormalized REE abundance is plotted against atomic number (Cornell, 1993; McLennan & Taylor, 2012).

REE concentrations increase when pH decreases. A shale-normalized REE concentration record of modern seawater measurements typically has certain characteristics, including (1) HREE enrichment and (2) a redox-sensitive Ce anomaly (Y. Zhao et al., 2022). Our proposed REE-pH proxy relies on pH-dependent HREE enrichment through REE scavenging and the fact that stability constants for REE complexes (mainly carbonates) increase with atomic number in the pH range 7.3–8.2 (Byrne & Kim, 1990; Schijf et al., 2015). Signatures (1) and (2) of seawater will be discussed in subsequent sections.

REE scavenging is the removal of REEs in seawater by sorption onto particulate “scavengers” such as organic matter, silicates, and other phases (reviewed by Y. Zhao et al., 2021). Scavengers pick up HREEs and LREEs unevenly, causing HREE enrichment and LREE depletion in seawater. The chief reason why LREEs are preferentially removed from solution is because free metal of LREEs is more abundant than the same species for a corresponding MREE or HREE. The free metal ion is more chemically reactive and, hence, is more available to complex onto the surfaces of Fe/Mn oxide/oxyhydroxide, organic matter particulates and be removed from the solution (Byrne & Kim, 1990; Cantrell & Byrne, 1987; Johannesson et al., 2006; Koeppenkastrop & De Carlo, 1992, 1993; Quinn et al., 2004; Schijf et al., 2015). The result is a positive relative trend when shale-normalized REE concentrations in modern seawater are plotted as a function of REE atomic number (Akagi, 2013; Byrne & Kim, 1990; Nishino et al., 2022; Nishino & Akagi, 2019; Schijf et al., 2015).

Marine limestones take up and preserve REY concentrations in seawater through accommodation of REY³⁺ at Ca²⁺ sites with a concentration distribution that depends on seawater pH (Byrne & Kim, 1990; Schijf et al., 2015; Y. Zhao et al., 2021). Therefore, we postulate that ancient marine carbonates should preserve a record of seawater pH via their relative concentration of REEs.

We assume shale-normalized REE concentrations increase linearly with atomic number (McLennan, 1989). An REE anomaly indicates that the measured concentration of an REE differs from the value based on linear projections of the neighboring element concentrations (Rollinson, 1993). We use an REE concentration ratio to express REE anomalies, for example, the La anomaly and Ce anomaly (Lawrence & Kamber, 2006; Tostevin et al., 2016; See Supplementary Data for derivation):

$$\text{La/La*} = \frac{\lbrack La\rbrack}{3\lbrack Pr\rbrack - 2\lbrack Nd\rbrack}\tag{2}$$

$$\text{Ce/Ce*} = \frac{\lbrack Ce\rbrack}{2\lbrack Pr\rbrack - \lbrack Nd\rbrack}\tag{3}$$

The numerator REE is the measured REE concentration, [REE], whereas the denominator REE* is the linear projection of the REE concentrations with similar atomic numbers. The REEs in the projection are not always adjacent. When the ratio is less than 1, the anomaly is a “negative” anomaly.

REE anomalies are extremely important to identify carbonate samples that show inadvertent extraction of non-carbonate fractions, diagenetic exchange, and non-marine depositional settings. (see also table 4 in Sec. 4.4). In modern seawater, large La anomalies (La/La*> 3, mole ratio) indicate open ocean settings (K.-J. Zhang et al., 2017), whereas a negative Ce anomaly normally indicates an oxidized ocean (Tostevin et al., 2016).

Although not an REE anomaly, Y/Ho ratios also indicate depositional environments. Lower Y/Ho ratios (Y/Ho < 44, mole ratio) indicate continental input and possible freshwater sources (Bau & Dulski, 1999; Satish-Kumar et al., 2021; Y. Zhao et al., 2022).

We demonstrate a proof-of-concept for a marine carbonate REE-seawater pH proxy using modern seawater and validate with published pH estimates derived from boron isotopes. Then we provide direct seawater pH estimates for some Neoproterozoic environments with REE concentration records from Precambrian marine carbonates. By looking at REE anomalies and trends, we discuss how accuracy of the REE-pH proxy can be affected by freshwater influence, siliciclastic input, and diagenesis, which suggests how marine carbonates might be screened to only select those that preserve the best pH proxy signal.

2. METHODS

2.1. REE scavenging and speciation

We first considered REE speciation in seawater based on how REEs are scavenged (Schijf et al., 2015). Concentrations of trivalent REE ions and carbonate complexes, which are the dominant species in seawater, depend on pH (Luo & Byrne, 2004). Hence, REE concentration in seawater becomes a function of pH.

We used PHREEQC, a USGS aquatic chemistry software (Parkhurst & Appelo, 2013), to compute REE speciation over a range of pH values. The speciation model includes the complexation reactions of major ion concentrations in a fixed total dissolved REE concentration (1 pmol/kg). The major dissolved species include cations (REE³⁺) and ligands formed with anions (especially CO₃^2-) at different seawater pH values. To model complexation reactions and speciation in seawater, we used the ion pairing constants and thermodynamic stability constants given in the REE scavenging model of Schijf et al. (2015). The code for the PHREEQC model is provided at the end of this paper (see Data Availability).

To estimate the REE enrichment trend of samples of modern seawater and records in the marine carbonate rocks, we define the REE-pH proxy as the pH-dependent slope of the best fit line of shale-normalized REE concentration in a sample as a function of REE atomic number. There are two advantages when using the slope of multiple REEs in the pH estimation: (1) The slope of multiple REEs is a quantitative value that shows the enrichment trend regardless of the absolute REE concentration. (2) Some REEs have anomalies so that these REEs are best omitted (e.g., Ce and Eu). Also, literature reports sometimes have missing values of some REEs that were not quantified, so using the slope of multiple but select REE values instead of individual REE measurements or two-element ratios ensures that the proxy can still consistently produce reasonable estimates of seawater pH without all REEs being measured.

We choose the seawater pH proxy to be a linear regression line of the concentration of four elements, Sm, Gd, Dy, and Er, omitting other elements, as we will explain shortly. We define the slope of this subset of elements versus atomic number (which includes the lightest MREE (Sm), heavier MREEs (Gd and Dy), and HREE (Er)) as the “REE slope.” We can derive the REE slope from an equation:

$$m_{i} = \alpha i + \varepsilon_{m}\tag{4}$$

Here, i is the corresponding atomic number of REEs (Sm, Gd, Dy, Er) (a.m.u); $\alpha$ is the REE concentration slope (a.m.u^-1); $m_{i}$ is the shale normalized REE concentration for the atomic number i (unitless) like in equation (1). Here, $\varepsilon_{m}$ is the vertical axis intercept of the regression best fit line (unitless, same unit as $m_{i}$). We solve for both $\alpha$ and $\varepsilon_{m}$ in the regression but focus on the slope $\alpha$.

We omit the other REEs because the REE patterns can be affected by anomalies from other mechanisms besides pH, such as Ce that is affected by redox in modern seawater (Elderfield et al., 1988). Table 1 shows the REEs and the reasons for filtering out certain elements. All REEs are affected by terrigenous sources as the continents are the primary source of REEs to the ocean. However, for ancient carbonates, some argue that local terrigenous sources affect LREE concentrations, and hydrothermal vents affect Eu concentrations, in particular (Bau & Dulski, 1999; German et al., 1990; Y. Zhao et al., 2022). Deep ocean water mass mixing can affect REE concentration systematically, as LREE depletion becomes less obvious in deep waters (Deng et al., 2017; Elderfield & Greaves, 1982). We also remove HREEs with an atomic number larger than Er (which includes Tm, Yb, and Lu) from our pH proxy because they are prone to be affected by water depth and show a negative concentration trend with increasing atomic number compared to the Er concentration (Piepgras & Jacobsen, 1992).

To examine how the REE slope changes with seawater pH, albeit over a limited pH range, we use the empirical depth-dependent pH changes of modern seawater and associated changes in the distribution of REE concentrations. We use dissolved REE concentration measurements from modern seawater in the GEOTRACES database, which includes a wide range of measurements in the Pacific and Atlantic oceans (GEOTRACES Intermediate Data Product Group, 2021). Because surface inputs and deep-water masses affect the REE concentrations, we chose subsurface seawater (200–800m) with monotonic pH and REE concentration change to filter out any aeolian or deep seawater REE input (Elderfield & Greaves, 1982).

We created a linear regression model using seawater pH from the Global Ocean Data Analysis Project (GLODAPv2), a NOAA database (Key et al., 2015; Olsen et al., 2016):

$$\alpha = \beta Y + \varepsilon_{\alpha}\tag{5}$$

Here, Y is the corresponding pH of seawater; $\beta$ is the slope of the best fit line in the linear regression model (a.m.u^-1pH^-1); $\alpha$ is the REE concentration slope (a.m.u^-1) like in equation (4) but explicitly for seawater. Here, $\varepsilon_{\alpha}$ is the vertical axis intercept of the REE slope (a.m.u^-1, same unit as $\alpha$). We solve for both $\beta$ and $\varepsilon_{\alpha}$ in the regression but focus on the slope $\beta$. Our goal is to use $\beta$, slope of the linear regression line for REE slope and pH to predict seawater pH, given the REE slope $\alpha$.

2.2. REE partition coefficients for limestone

The pH-dependent REE concentrations in seawater will be reflected by uptake in sedimentary marine carbonates and may be altered in their relative levels by partitioning between the carbonate and seawater. If we know the partition coefficients, we can estimate seawater REE/Ca from REE concentration records in marine carbonates, and thus derive the REE concentrations in rocks with the Ca concentration known in rocks and assumed for ambient seawater. The standard way to quantify REE partitioning between seawater and marine sediments is to use empirical partition coefficients. The definition of the trace metal partition coefficient follows Henderson and Kracek (1927):

$$m_{REE} = \frac{X_{REE}}{D_{REE}} \cdot \frac{m_{Ca}}{X_{Ca}}\tag{6}$$

Here, m is the molality (mol/kg) of the element concentration in seawater, either the dissolved REE (m_REE) or aqueous calcium cation (m_Ca), and X is the molar ratio of the element concentration in carbonate rock samples, i.e., X_REE = mol REE/total moles in the rock. D_REE is the partition coefficient of REEs in an aqueous solution (unitless).

Partition coefficients range from 10^-1 to 10³ (Smrzka et al., 2019). This wide spread corresponds to the initial setup of measurement experiments and comes from different experiment settings and REE incorporation processes (Möller & De Lucia, 2020; Morse et al., 2007). However, the relative partition coefficients between different REEs mostly remain constant for a given setup, which shows a flat pattern when plotted against atomic numbers (Nishino et al., 2022; Toyama & Terakado, 2019). Hence, the REE slope should still be useful for estimating the pH from limestone REE concentrations. Table 2 shows the variables X_REE, D_REE, and m_Ca⁄X_Ca that we used from the literature to derive m_REE, which resembles the estimated seawater REE concentration (Toyama & Terakado, 2019). We calculate the REE slope $\alpha$ for estimated seawater from marine carbonate REE records using equation (4) and their corresponding pH by applying the $\alpha$ values to equation (5) with the $\beta$ calibrated from seawater.

Petrographic, mineralogical, and geochemical screening of potential samples is critical for the marine carbonate selection used to estimate seawater pH. We estimated pH values for five Phanerozoic samples mentioned in Toyama and Terakado (2019), where they mainly consist of calcite and come from reefal depositional environments (Kawamura, 1989; Kobayashi, 2002; Nakamori et al., 1991; Ota & Isozaki, 2006; Ujiié, 1994). The five samples have low Al, Mn, and Fe concentration, when compared to primary signals of dissolved bulk carbonates (Toyama & Terakado, 2019; K. Zhang et al., 2015). We excluded the two samples (YK-1 & FJ-1 in Toyama & Terakado, 2019) possibly affected by Fe-Mn oxides and filtered out KD-1 because it consists of dolomite.

Modern seawater has a limited but variable pH range. To test if the REE-pH seawater proxy works on a wider range of pH values, we also compared REE-pH proxy estimates with pH estimates from boron isotopes in the geologic record (Foster & Rae, 2016). The 𝛿¹¹B isotope seawater pH proxy gives pH estimates across the Cenozoic, 66 Ma-present (Rae et al., 2021).

Equations (1), (4), (5), and (6) are a system of four equations with four unknowns: the shale-normalized REE concentration $m_{i}$ in carbonate rocks, REE slope $\alpha$, REE-seawater pH linear regression slope $\beta,$ and the REE concentration in ancient seawater, $m_{REE}$. We solve this system of equations to estimate seawater pH using REE concentrations from marine carbonates.

3. RESULTS

3.1. REE speciation and pH

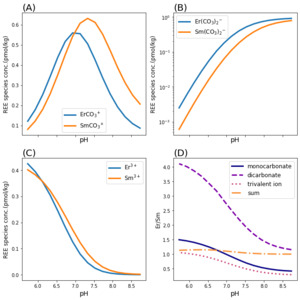
Figure 1 shows the dominant species of Sm, Gd, Dy, and Er in modern seawater over a range of pH on either side of neutral (pH 5.7–8.7) according to our PHREEQC model. This range covers the quasi-neutral pH estimates from Grotzinger and Kasting (1993) and Krissansen-Totton et al. (2018). The dissolved REE molal concentration of trivalent ions (REE³⁺), monocarbonato complex (REECO₃⁺), and dicarbonato complex (REE(CO₃)₂^-), is divided by the fixed total dissolved REE concentration (1 pmol/kg) in seawater to give a unitless ratio. Clearly, the dissolved REE species change considerably as a function of pH from acidic to alkaline. Supplementary table 1 shows the complete REE concentration speciation.

Figure 1.The concentration of three dominant species of the four REEs (Sm, Gd, Dy, Er) used in the pH proxy in seawater. The dominant species of REEs in seawater, trivalent ions, monocarbonato-complexes, and dicarbonato-complexes, change as seawater pH changes. Other REE complexes with ligands such as chloride (Cl^-) and sulfate (SO₄^2-) exist in seawater but have less quantity in pH range above 6 so they are not included in the figures. The values were calculated using PHREEQC and REE speciation constants from Schijf et al. (2015).

To evaluate the HREE enrichment change of REE concentrations, we focus on the relative REE enrichment trend instead of individual REEs. Specifically, the HREE enrichment and LREE depletion change with pH. As mentioned in the Introduction, HREE/LREE ratios indicate HREE enrichment. Figure 2 shows that HREE enrichment in seawater depends on pH in the REE speciation model within the pH range of 5.7–8.7. In particular, although the dicarbonato ligand begins to dominate in alkaline conditions for both HREE and LREEs, the ratio of most HREE/LREE monotonically decreases when seawater pH increases, so we should expect the slope of REE concentrations versus atomic number to decrease with increasing pH. Which dissolved species (ligands) are incorporated into depositional carbonates is debated, but our results show that all three major species in seawater (trivalent ions, monocarbonato complex, and dicarbonato complex) change as pH changes (Curti et al., 2005; Elderfield et al., 1990; Goldstein & Jacobsen, 1987, 1988a, 1988b; Voigt et al., 2017). The Er/Sm ratio starts to plateau at highly alkaline or highly acidic conditions, albeit still monotonic.

Figure 2.Er/Sm, an example of HREE enrichment that decreases as seawater pH increases (See Supplementary figure 1 for all REE HREE/LREE ratios). The Er and Sm ligand and trivalent ion concentrations are calculated using PHREEQC and REE speciation constants, which are the same as figure 1 (Schijf et al., 2015). The trivalent ion and dominant REE complexes in seawater show concentration slopes that change as pH increases from 5.7–8.7. (A) monocarbonato complex concentrations between Er and Sm (B) dicarbonato complex concentration comparison between Er and Sm; the vertical axis is a log scale to show the contrast between the concentrations around pH=6. (C) Trivalent ion concentration comparison between Er and Sm. (D) The total Er/Sm ratio comparison of the three ions in (A), (B), and (C), and the sum of the combined Er/Sm ratio of (A), (B), and (C). The curve of the sum is in Supplementary data (Supplementary fig. 4)

3.2. Calibration of the pH proxy using seawater

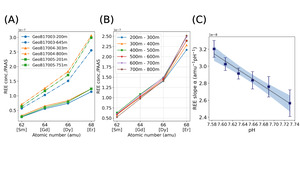
We calibrated the seawater pH proxy using shale normalized REE concentrations in the GEOTRACES database. Because the depth of the REE concentration measurements vary at different locations, we calculated the average seawater pH and REE slopes ($\alpha$) in each vertical profile by 100 m intervals from 200 m to 800 m over which the pH decreases from ~7.75 to ~7.6. Figure 3A shows a subset of data from GEOTRACES and how the REE slope changes. In fig. 3B, when considering the REE concentrations over global averages, pH affects the slope of MREEs (Sm, Gd, Dy), the slope is dominated by HREE (Er) versus MREE sensitivity to pH.

Figure 3.The REE-pH seawater pH proxy calibrated using modern seawater pH and REE concentrations. (A) Shale-normalized REE concentration measurements from individual seawater profiles with depths closest to 200 m and 800 m. The profiles are from the GeoB17 Stations 3, 4 and 5 from the GEOTRACES database (Behrens et al., 2018). (B) Average global shale normalized REE concentrations (Sm, Gd, Dy, Er) from GEOTRACES at different depths (443 measurements) where pH typically decreases with increasing depth. (C) REE slope ($\alpha$) versus pH derived from modern seawater. The solid line is the linear regression model (with slope $\beta = - 3.99 \pm 0.73 \times 10^{- 8}$) based on the REE slopes $\alpha$ calculated from figure 3B with equation (4) (R-squared = 0.97). The blue area is the 2σ confidence interval, which indicates the range of REE slopes that could fit existing pH values. The error bars are the 2σ standard error of the mean pH and mean REE slope values (Supplementary fig. 5).

We calculate the REE-seawater pH proxy $\beta = - 3.99 \pm 0.73 \times 10^{- 8}$ (2σ) from equation (5). The linear regression model (with slope $\beta$) in figure 3c indicates a negative relationship between REE slope and seawater pH, which is similar to HREE enrichment in the speciation model (fig. 2).

In this study, we focused exclusively on contemporary seawater values. However, variations in alkalinity, dissolved inorganic carbon (DIC), turbidity, and ionic strength across different oceanic systems during historical periods and among distinct water masses may alter the relationship between REE concentrations and pH levels derived from equation (5) (see also the terrestrial water references mentioned in Section 4.4).

3.3. Estimates of pH from Phanerozoic limestone

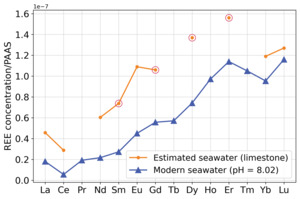
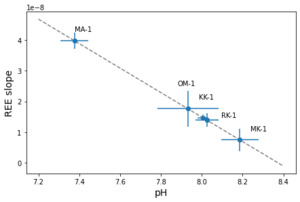
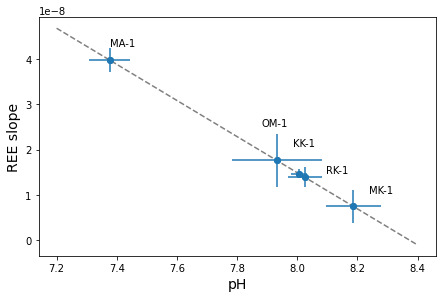
Using our proposed REE pH proxy of the slope of shale-normalized Sm, Gd, Dy, and Er concentrations, we computed five pH estimates ranging from 7.4 to 8.2 for limestone samples published by Toyama and Terakado (2019), where the empirical calcite partition coefficients are from. Toyama and Terakado (2019) also measured the same samples using different analytical techniques, which can cause differences in the REE concentrations measured in the analysis (See Section 4.3). In future studies, one could utilize a more extensive dataset encompassing published records spanning Precambrian periods (K. Zhang & Shields, 2022). The five limestones are located near the Pacific coast of Japan and range in age from Carboniferous to Quaternary. Our estimated seawater pH from the Quaternary sample is 8.03±0.06 (±2σ), roughly matching modern seawater with pH=8.1 (fig. 4). The Ce anomaly, LREE depletion, and HREE enrichment resemble modern seawater REE patterns in the REE concentration plot (Toyama & Terakado, 2019). The REE slope and corresponding pH estimate for all the limestone samples are shown in figure 5. The most acidic pH estimate with pH=7.38±0.07 (2σ) is from the Middle-Late Permian limestone sample MA-1, at the time of the Guadalupian–Lopingian Boundary (Ota & Isozaki, 2006). The lower pH possibly reflects the increase in pCO₂ at the Guadalupian–Lopingian Boundary, a time of increased volcanic activity (Foster et al., 2017; W. W.-Q. Wang et al., 2023).

Figure 4.Calculated REE concentrations in Quaternary seawater vs. directly measured REE concentrations in modern seawater normalized to the Post Archean Australian Shale (Pourmand et al., 2012). We used the REE partition coefficient equation (eq 6) defined by Henderson and Kracek (1927) to calculate REE concentrations in seawater using quaternary limestone and calcite partition coefficients as input (blue line; sample RK-1 of Toyama and Terakado (2019)). The circled dots are the elements Sm, Gd, Dy, and Er used in the REE-pH estimation (See Methods section). The orange line shows REE concentrations in modern seawater with pH = 8.02 at 198 m (REE data from GeoB17003 in Behrens et al., 2018; pH measurements from GLODAPv2 at the same location).

Figure 5.The pH estimates using REE concentration slope. The ages of the limestone samples range from Carboniferous to Quaternary (Toyama & Terakado, 2019). The gray line is the linear prediction model based on modern seawater measurements (same as the regression line from fig. 3C). The blue dots are the pH estimates for the marine carbonates based on the regression of modern seawater measurements. The labels represent the REE records in Toyama and Terakado (2019). MA-1 is Middle-Late Permian, RK-1 is Quaternary, OM-1 is Carboniferous, KK-1 is Middle Permian, and MK-1 is Neogene. The uncertainty comes from slope calculation for linear regression. The error bars for each data point are 2σ.

3.4. Validation of the REE-pH proxy using independent pH estimates from boron isotopes

To test if the REE-pH seawater proxy produces comparable results to other paleo seawater pH estimates, we compared pH estimates of the REE-pH proxy with pH estimates from the boron isotope seawater pH proxy (Rae et al., 2021). The Cenozoic boron isotope pH estimates span from 66–0 Ma, but some epochs within the Cenozoic era, such as Oligocene and Paleocene, lack data (Rae et al., 2021).

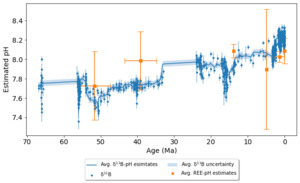
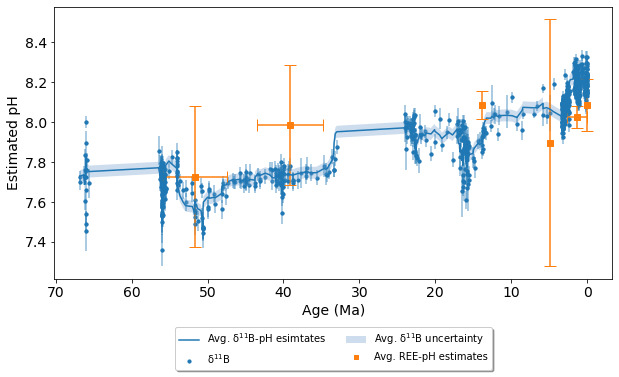
We estimated the pH of six marine carbonate formations from the literature with samples that overlap the timestamps of 𝛿¹¹B-pH estimates. figure 6 shows REE-pH estimates for Holocene, Quaternary, and Eocene carbonates with corresponding 2σ uncertainty. Table 3 lists the samples from the marine carbonate formations, including limestone and dolostone. The highest pH estimate is from the Holocene Heron Reef, with pH = 8.08±0.13, and the lowest is from the Eocene Khuiala formation, with pH = 7.73±0.35. All pH estimates match the 𝛿¹¹B-pH estimates within 2σ uncertainty, although the pH estimate from the Pliocene Pedro Castle formation has a large uncertainty (±0.62).

Figure 6.The comparison between pH estimates from 𝛿¹¹B isotopes. The blue dots are the B isotope pH estimations from Rae et al. (2021). The error bar shown in the blue shading for the 𝛿¹¹B-seawater pH estimates is 2σ. The orange squares are the pH estimates for limestone formations. The error bar for the pH estimates is 2σ.

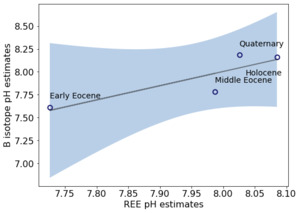
We next selected REE concentrations from four of the six limestone formations (Heron Reef, Minatogawa, Fulra, and Khuiala formations (see table 3)) to examine the correlation of pH inferred from REEs and boron isotopes. The Pliocene and Middle Miocene carbonates from H. Zhao and Jones (2013) were excluded because the majority of these samples from formations in the Cayman Islands are mixtures of limestones and dolostones and also may have a riverine influence (see Sec. 4.4). The dolostones might not produce accurate pH estimates because we are using limestone REE partition coefficients in the pH proxy. We then compared the REE-pH estimates with the 𝛿¹¹B-pH estimates of the same timestamps in the Holocene, Quaternary, and Eocene. The pH inferred from the REEs in the four limestone formations moderately correlates with 𝛿¹¹B-pH estimates with a linear regression slope of 1.6±1.3 (2σ) and R² of 0.75 (fig. 7). The confidence interval (blue region) 2σ indicates the uncertainty of the correlation of the four samples. We note that the lower pH range is limited to the one Eocene sample and clearly the relationship would be more robust were there more data to compare. Given the lack of accurate age estimates for individual samples, we assume that average pH values represent the average time window for a formation (e.g. Ypresian). The correlation of the pH values might change if more precise age estimates were known.

Figure 7.Preliminary pH estimates from REE in carbonates compared to pH estimates inferred from B isotopes. The solid line indicates the correlation between REE-pH and 𝛿¹¹B pH estimations. The blue area is the 2σ confidence interval, which indicates the range of slopes that could be fit to existing pH estimates. The R-squared value for the data is 0.75.

3.5. Preliminary Application to Precambrian samples

Next, we demonstrate that the REE-pH proxy could provide rough estimates from carbonates that demonstrate a postglacial open-ocean setting deposited in the early Ediacaran periods (Rodler et al., 2016). The REE-pH estimates for the Neoproterozoic Snowball Earth carbonates are from the same carbonate formation group (Otavi Group, Namibia) that Kasemann et al. (2010) assessed with boron isotopes. The age of the Otavi Group is from 770 Ma to 580 Ma (Halverson et al., 2005). Here, we use the REE concentration data from the Keilberg and Maiberg formations at the Fransfontein sampling profile at the Otavi Group (Rodler et al., 2016).

Figure 8 shows 11 pH estimates of the Keilberg and Maieberg formations and the corresponding 𝛿¹¹B values (Kasemann et al., 2010; Rodler et al., 2016; See Supplementary table 2 for the complete list of carbonate samples used for REE-pH estimates). We filtered out one sample FSF-25 with a large error bar (ΔpH>7). The Keilberg and Maieberg formations indicate shallow marine depositional settings (Hoffman, 2011; Rodler et al., 2016). Both REE-pH estimates and 𝛿¹¹B-pH estimates start with higher than neutral pH values at the Keilberg formation samples and decrease in the following Maieberg formation samples.

Figure 8.Comparison between pH estimates from REEs and 𝛿¹¹B in early Ediacaran carbonates in the Keilberg and Maieberg formations at the Fransfontein profile, Namibia (Kasemann et al., 2010; Rodler et al., 2016). The vertical axis is the sample height in meters. We adjusted the sample heights from their references so both REE-pH estimates and 𝛿¹¹B records start where the Ghaub formation ends. The Keilberg and Maieberg formations are from post-glacial environments after the Marinoan glaciation. The first data point of the REE-pH estimates and the samples with 0-4.6m depths are the Keilberg formation. For REE-pH estimates, the data points highlighted in orange are limestone, while the remaining samples are dolostones. The uncertainty is 2σ for each REE pH estimate and 𝛿¹¹B data point, and the 2σ uncertainty for 𝛿¹¹B-pH estimates are inferred from the calibration for 𝛿¹¹B isotope (see Data Repository from Kasemann et al. (2010) and Ohnemueller et al. (2014)).

4. DISCUSSION

4.1. REE-pH estimate uncertainty

The accuracy of the REE-pH estimates relies on preserving the seawater REE signatures in marine carbonates, and the size of the error bars in figure 6–8 are not small. Diagenetic processes, including freshwater and siliciclastic input, can alter the REE distribution, potentially spreading the pH estimate (Azmy et al., 2011; Srivastava & Singh, 2019; Y. Zhao et al., 2022). The quality of the pH estimates relies heavily on the extent to which marine carbonate samples retain primary REE signatures of seawater only. Here, we discuss factors that possibly influence the REE-pH proxy and the prediction results. The potential factors of uncertainty are model calibration, acid treatment to extract REE from carbonate samples, freshwater sources, siliciclastic input, and diagenesis.

4.2. The uncertainty from model calibration

The REE-seawater pH proxy is calibrated from modern seawater only over a range of ~7.58 to ~7.73 (Sec. 3.2). This pH range is derived from subsurface seawater, which is likely different from the surface where most Precambrian marine carbonates are deposited. However, we assume that the REE-pH proxy extrapolates linearly over the weakly acid to the weakly alkaline range of pH given the changes in carbonate complexation predicted by the PHREEQC model results (fig. 2). This assumption is supported by the matches to pH estimates from 𝛿¹¹B isotopes. The linear correlation between REE-pH estimates and 𝛿¹¹B isotopes is driven by the Eocene Khuiala sample, which has a lower REE-pH estimate value of 7.73 (fig. 7), Therefore, the inclusion of pH estimates in between the range of 7.73 to 7.90 for REE-pH proxy that overlaps the age of 𝛿¹¹B isotope pH estimates would make the positive relationship more statistically robust. The assumption of the linear correlation outside of the modern seawater pH range remains as an uncertainty for the paleo-seawater pH estimates.

Z.-L. Wang et al. (2013) proposed a three-stage linear relationship model for freshwater between REE concentration (La) and pH where the linear relationship flattens out above pH 7.5. It is possible that the slight REE concentration increase after pH 7.5 skews the linear relationship between REE slope and pH (fig. 2D, where the Er/Sm curve is flatter above pH 7.5 compared to lower pH).

It is possible that other factors, such as degrees of ocean mixing, affect REE patterns at the subsurface. We examined the correlation between the Ce anomaly and the Y/Ho ratio and the REE slope at different depths (Supplementary fig. 6). Y/Ho shows a low correlation, whereas Ce anomalies correlate with the REE slope and dissolved oxygen at different depths. In anoxic and suboxic conditions, the most dominant control on Ce anomalies is likely dissolved oxygen, but in oxic open oceans, the Ce anomaly is likely to reflect the REE adsorption chemistry (Cao et al., 2022). The high correlation between the Ce anomaly and oxygen from the global average seawater data, mostly from open oceans, could be a mixed result of pH, dissolved oxygen, and other factors influencing the Ce anomaly.

4.3. The difference in analytical protocols

The REE data from marine carbonate are likely robust against different measurement techniques. Different analytic protocols for the REE concentration analysis in marine carbonates, such as using HCl or acetic acid to dissolve the samples, can cause differences in the REE concentrations. However, the samples we analyzed have no significant difference in the REE slope (fig. 9).

Figure 9.The Pearson’s R correlation between REEs in limestone and dolostone dissolved in HCl and acetic acid solutions during experimental analysis to derive REE distributions. The pH estimates are highly correlated (R² = 0.96), showing that the different reagents have minimal impact on the REE slopes and the pH estimates (Toyama & Terakado, 2019).

4.4. Freshwater influence and siliciclastic input

The location of carbonate deposition matters for providing reliable primary seawater REE signals. The REE concentration plots should typically show the signatures such as a Ce anomaly for oxygenated waters, LREE depletion, and HREE enrichment that resemble modern seawater. A flatter, MREE-enriched REE concentration plot can occur in places with freshwater inputs, such as river deltas and estuaries (Alibo & Nozaki, 1999). Marine carbonate samples with La/La*<2 indicate possible freshwater influence (Lawrence & Kamber, 2006; Y. Zhao et al., 2022). Table 4 shows a list of seawater REE anomalies from the literature.

In REE concentration records from H. Zhao and Jones (2013), which we listed in table 3 but excluded from figure 7 analyses, the marine carbonate formations are in the Caribbean Sea, a region close to freshwater REE input from river deltas (Osborne et al., 2015; H. Zhao & Jones, 2013). The freshwater input and water body mixtures at estuaries increase the uncertainty of the pH estimates from the carbonate formations in this region. The Sahara dust brings in aeolian REE input into the surface seawater, which could also cause MREE enrichment, but not affect HREE/LREE enrichment (Elderfield & Greaves, 1982; Osborne et al., 2015). Li et al. (2017) pointed out that LREE enrichment in marine carbonates could indicate freshwater influence. However, terrestrial waters are commonly enriched in the HREEs over the LREEs when compared to shale composites for the very same biogeochemical reasons that seawater is, which is explained by the competition between aqueous complexation and surface complexation (e.g., Adebayo et al., 2018; Johannesson et al., 1999, 2000, 2005, 2006; Tang & Johannesson, 2006). HREE-enriched patterns develop in rivers and estuaries, including subterranean estuaries, where the freshwater endmembers are commonly highly enriched in the HREEs compared to the LREE when normalized to shale composites (Adebayo et al., 2020; Chevis et al., 2015, 2021; Davranche et al., 2015; Elderfield et al., 1990; Hoyle et al., 1984; Johannesson et al., 2011, 2017; Sholkovitz, 1995). It would be challenging to identify the depositional environment based on only the REE patterns.

In the Silurian to Quaternary carbonates that we analyzed in figure 5, some of the REE concentration records lack Pr data, which is the neighboring element (alongside Ce) required to calculate the La anomaly (see eq. 2). Hence, although the La anomalies are positive, the magnitudes of La anomalies are uncertain. The lower Y/Ho values of the Eocene samples suggest possible freshwater influence (Srivastava & Singh, 2019).

The Eocene marine carbonate samples from Patra and Singh (2017) and Srivastava and Singh (2019) in table 3 both show modern seawater REE signatures despite the total REE concentration being systematically higher than the total REE concentration of modern seawater (fig. 10). There is also less LREE depletion in the Eocene marine carbonate samples compared to the modern seawater measurements of the same pH.

Figure 10.Comparing REE concentrations of marine carbonates samples and modern seawater with similar pH in the North Pacific. REE concentrations from TPS 24 271-1 (184m and 640m; Piepgras & Jacobsen, 1988). Seawater pH values for the corresponding depths are interpolated from GLODAPv2 at 24.29 °N, 150.463 °E, close to TPS 24 271-1. (pH 7.97 at 184 m and pH 7.56 at 640 m depth from GLODAPv2). The average REE concentrations are from the two Eocene carbonate formations with larger uncertainties in figure 6 (Patra & Singh, 2017; Srivastava & Singh, 2019). We interpolated the missing values for seawater REE concentrations. The depletion in some HREE concentrations (Tm, Yb, Lu) is a common pattern seen in shallow seawater (e.g., fig. 4).

The two sets of Eocene samples show REE anomalies that increased the uncertainty of the pH estimates (fig. 11; See the Introduction section for the definition of REE anomalies). The Sm anomaly (Sm/Sm*, See Supplementary Data for calculation) in the early Eocene Khuiala formation samples are from 0.85 to 1.10, similar to the Sm/Sm* values of the mid-Eocene Fulra formation samples. Sm anomalies are not prominent signatures of specific geochemical processes in modern seawater.

Figure 11.(A) The REE concentrations of 12 carbonate samples of the Khuiala formation from early Eocene represented by each colored line. Patra and Singh (2017) suggest that Khuiala formation limestones in the Jaisalmer Basin are affected by siliciclastic sediments. In general, REE samples with higher REE concentrations are likely to have more siliciclastic input. (B) The REE concentrations of the 12 carbonate samples of the Fulra formation from the Middle Eocene are represented by each colored line. Middle REE enrichment (or flat REE patterns) could indicate freshwater influence or estuary environments. However, the reason behind the negative Er anomaly in these limestone samples is unclear (Srivastava & Singh, 2019).

Positive Dy and negative Er anomalies are also found in Fulra formation samples. When considering relative enrichment compared to other REEs, Dy, and Er anomalies can signify freshwater influence or detrital input (MREE enrichment, fig. 11). The sensitivity of REE patterns towards detrital content in carbonates is high, with 0.1 to 1% of detrital components capable of masking parent fluid REE distribution in carbonates (Schier et al., 2021). Hence, phase-specific sampling of marine carbonate cement may be a safer way to circumvent detrital influence. Here, Gd, Dy, and Er anomalies may increase the uncertainty of the pH estimation, but because most of the records still show seawater signatures and consistency, the measurements and pH estimates should still be a rough estimate for Eocene seawater (Patra & Singh, 2015, 2017; Srivastava & Singh, 2019).

Our pH estimation is based on the average REE slopes of each marine carbonate formation. Therefore, a small sample size of some formations affects the pH estimates. Because of the variance in the carbonate samples in each formation, outliers can skew the pH estimates and increase the uncertainty of the pH estimates. However, even with a limited sample size from a carbonate formation, the uncertainty is constrained by filtering out REEs with known anomalies when calculating the REE slope, as described in table 1.

Another limitation is that we are estimating pH using empirical calcite partition coefficients. In many sedimentary formations, the samples can be mixtures of different marine carbonates such as limestone, dolostone, and aragonite. The calcite partition coefficients from limestone show similar patterns and are in the same order of magnitude (10²), whereas partition coefficients derived from coral show a similar flat pattern but have much lower values than the ones from limestone and microbiolite (Johannesson et al., 2014; Toyama & Terakado, 2019; Webb & Kamber, 2000). This suggests the pH proxy is most accurate where samples are phase specific, and the mixture of different materials will increase the pH uncertainty and possibly require different partition coefficients.

4.5. Diagenetic alteration

The effect of diagenesis on REE concentrations in marine carbonates can vary. Multiple studies point out that REEs are relatively immobile during diagenetic alteration, as the ΣREE does not significantly change in the same formations that consist of different types of marine carbonates (A. v. S. Hood et al., 2018; Srivastava & Singh, 2019; Webb & Kamber, 2000; H. Zhao & Jones, 2013). However, diagenesis in the early deposition stage can alter the primary REE seawater signatures of marine carbonates (Y. Zhao et al., 2022). Depending on the openness of the diagenetic system REE patterns may be entirely replaced by circulating diagenetic fluids (Higgins et al., 2018; Zwicker et al., 2018). Because of diagenesis, petrographic screening for sample selection, as suggested by the work of Hood and Wallace (2012), for example, is a prerequisite for geochemical analyses.

Possible diagenetic alterations for limestones include neomorphism (i.e., aragonite to calcite) and dolomitization. Neomorphism (meteoric) retains most of the seawater REE signatures with slight LREE depletion that will be filtered out by our selection of REEs to use for calculating the slope of the REE distribution, giving minimal effect on the derivation of pH (Webb et al., 2009).

Dolomitization can change the total abundance of the REE concentrations, but they still retain the REE concentration patterns in the marine carbonates (Banner et al., 1988; Y. Zhao et al., 2022). The reason is that dolomitization and recrystallization do not alter REE concentrations and REE signatures when dolomitization happens under seawater without hydrothermal influence (L. Wang et al., 2014; H. Zhao & Jones, 2013). Hence, some dolostones can preserve the REE signature in the precursor limestones (Miura & Kawabe, 2000).

Our results show that dolomitization has little to no correlation with REE concentration and REE slopes. We filtered out most of the REE anomalies in the REE slope model, so the REE slope itself should remain relatively unaffected by changes of individual REE changes for dolomitization such as La, Ce, Eu, Y/Ho anomalies (Y. Zhao et al., 2022). As a result, the REE-pH estimates should remain relatively robust. Although dolomitization has a low correlation to REE-pH estimates, we used empirical calcite partition coefficients for our REE-pH estimates. The immobility of REE concentration would benefit REE slope estimation but would require another set of empirical dolomite partition coefficients likely representative of an open ocean water setting. Therefore, we did not include the dolostone containing Cayman Island carbonates from H. Zhao and Jones (2013) in Figure 7 because we focus on samples with marine carbonates with known empirical partition coefficients.

4.6. Estimates of pH for Precambrian marine environments

The goal of this paper has been to demonstrate a proof-of-concept REE-pH proxy capable of estimating Precambrian seawater pH to within 1 to 2 pH units. Relatively high uncertainty of the pH is expected given the complexity of depositional environments in Precambrian seawater and the scarcity of marine carbonates that indicate a shallow and open ocean environment (Cantine et al., 2020; Also see REE-pH estimate uncertainty in the Discussion). Therefore, carbonate sample selection and identifying diagenesis is important. However, to constrain the current range of Archean seawater pH estimated with a range from the boundary conditions pH = 4 to pH >10, a crude pH proxy with an uncertainty of ΔpH ~ 1.5 is sufficient.

In this paper, we assume a fixed alkalinity value for modern seawater because the carbonate samples we analyze are relatively modern. The alkalinity was possibly higher in Archean based on [Ca²⁺] abundance (Cantine et al., 2020; Grotzinger & Kasting, 1993; Kempe & Degens, 1985; Ronov, 1964, 1968). For Archean pH estimates, the alkalinity of seawater could be better constrained by modeling the alkalinity as a function of [Ca²⁺] (Krissansen-Totton et al., 2018). For example, in the nominal model of Krissansen-Totton et al. (2018), median [Ca²⁺] increases monotonically by a factor of ~2.5 going backwards in time from the present value (0.01 mol/kg) to 4 Ga.

In validating REE-pH estimates versus those derived from 𝛿¹¹B in the Cenozoic, the ages of 𝛿¹¹B-pH were interpolated. Exact overlapping ages are scarce, so the difference between the REE-pH estimates and the 𝛿¹¹B-pH estimates is also affected by the paucity of suitable samples and mismatch in the ages of the carbonate formations from which REE distributions are known (fig. 6).

In figure 8, the REE-pH estimate shows a negative excursion similar to the 𝛿¹¹B-pH estimates at the start of the Maieberg Formation, with the minimum pH at sample height 58.5m and 48.2m, respectively. However, the pH decrease from the REE-pH estimates is larger than the pH decrease indicated by 𝛿¹¹B-pH estimates.

For the 𝛿¹¹B-pH estimates, there may have been changing boron isotope composition in the cap carbonates due to the mixing of meltwater and syn-glacial seawater, which adds uncertainty that the boron isotope is not only reflecting the change in pH (Ohnemueller et al., 2014; Shields, 2005; Yu et al., 2020).

The mixture of the materials in the Fransfontein site samples between the glaciation episodes may have increased the uncertainty and accuracy of the pH estimates (Rodler et al., 2016). Positive Eu anomalies suggest hydrothermal influence. Like the REE concentrations of the Fulra formation from Mid Eocene in figure 11, Er anomalies can be a sign of freshwater influence (fig. 12). When the magnitude of the anomaly is significant, the uncertainty of the pH estimates will increase, for example, FSF-26, the largest uncertainty from the Fransfontein profile has a ΔpH ~3.

Figure 12.The Fransfontein marine carbonate samples show unexpected Er anomalies, suggesting possible influence by freshwater or hydrothermal input, which creates larger uncertainty for the pH estimates (German et al., 1990; McLennan & Taylor, 2012).

The uncertainty that freshwater creates for the seawater pH proxy depends on the REE patterns and anomalies from the freshwater. An enrichment in LREE/MREE decreases the REE slope and may lead to the REE-pH proxy underestimating the pH, whereas a depletion in HREE (e.g., negative Er anomaly in fig. 12) may lead to the REE seawater pH proxy overestimating the pH.

5. CONCLUSION

Our results suggest that the REE concentrations in most limestones can be a seawater pH proxy with a 2σ uncertainty ranging over 1 to 1.5 pH units. We defined a REE-seawater pH proxy based on a pH-dependent “REE slope,” which is the relative HREE/LREE enrichment trend of shale-normalized REE concentrations in marine carbonates. We use the elements of Sm, Gd, Dy, and Er to define the slope, which generally avoids REEs strongly affected by factors other than pH. With the REE slope method, we estimated the pH values of 13 limestone formations, including those from Toyama and Terakado (2019). The REE-seawater pH proxy agrees with most pH estimates derived from δ¹¹B data in the Cenozoic and Ediacaran to ~1.5 units of pH. Hence, the REE-seawater pH proxy is likely sufficient to distinguish competing hypotheses about whether early Earth’s oceans were moderately acidic (pH = 4) or highly alkaline (pH > 10).

The primary concern about the REE slope concept is the uncertainty of pH estimates caused by noise in the REE slope introduced by freshwater input, siliciclastic input, and diagenesis, such as dolomitization. The uncertainty could be constrained better with more understanding of the factors that can alter the REE concentration and the depositional history of the carbonate samples.

We did not extensively explore dolomite as a pH proxy in this paper. However, many Precambrian carbonates are dolostones, so the proxy needs to be further investigated to assess how it might apply to predominantly dolomitic mineralogy (Cantine et al., 2020; A. V. S. Hood & Wallace, 2012; Smrzka et al., 2019). Besides marine carbonates, banded iron formations (BIFs) are also commonly used as a reliable Precambrian environmental proxy (Konhauser et al., 2017; Planavsky et al., 2010). However, the BIFs are not as widely distributed in space and time as marine carbonates through the Precambrian (e.g., missing the mid-Proterozoic) and likely require a different approach for calibration when compared with modern seawater.

The REE slope concept is a promising candidate for a seawater pH and would complement existing proxies such as boron isotopes to give more context to the Precambrian environment. Future work includes identifying diagenetic alteration in Proterozoic and Archean marine carbonate samples and developing a refined screening protocol for sample sets to produce a time series of seawater pH estimates.

DATA AVAILABILITY

The source code is available at https://github.com/PingChunLin/REE_pH.git.

AUTHOR CONTRIBUTIONS

Ping-Chun Lin: Data Collection, Data Analysis, Writing - Original Draft. David Catling: Research Proposal, Supervision, Writing - Review & Editing.

ACKNOWLEDGMENTS

The authors acknowledge funding from Simons Foundation grants 511570 and 511570FY20 to DCC. We thank Karen Johannesson, Graham Shields, one anonymous reviewer, and Associate Editor Timothy Lyons for knowledgeable, constructive comments that greatly improved the manuscript. The authors thank Jonathan Toner for help in setting up the PHREEQC model. P-CL also thanks Nicholas Wogan, Joshua Krissansen-Totton, and Marjorie Cantine for helpful discussions and comments on the paper.

DATA AND SUPPLEMENTARY INFORMATION

Please see the data, supplementary figures, tables, and documents at: https://doi.org/10.5061/dryad.69p8cz99r

Editor: C. Page Chamberlain, Associate Editor: Timothy Lyons